We reviewed and arrived back at the problem we were considering last Wednesday -- Guess a number with only four possibilities: 0, 1, 2, and 3, having the following probabilities: 1/2, 1/4, 1/8 and 1/8. The Old Approach divides the possibilities in half with each "binary" question and guarantees a result in two guesses. The New Approach divides the probablitites in half and gets the answer in one guess half the time, in two guesses a quarter of the time, and in three guesses another quarter of the time. So that the expected number of guesses N_guess is

N_guess = (1/2)(1 guess) + (1/2)(2 guesses) + (1/8)(3 guesses) + (1/8)(3 guess) = 1.75 guesses

We further related the number of guesses {1, 2, 3, 3} above to the corresponding probabilities {1/2, 1/4, 1/8, 1/8} through number of guesses is -Log₂(probability) So putting these pieces together results in

N_guess = - p₀ Log₂(p₀) - p₁ Log₂(p₁) - p₂ Log₂(p₂) - p₃ Log₂(p₃)

N_guess = ∑_p - p Log₂( p )

Since the number of guess corresponds to the information corresponds to the (information) entropy, this is the formula for entropy.

We discussed some of the names associated with this field. Benjamin Thompson (Count Rumford) made the association between work and heat -- more boring of the cannon (and hence more work) produced more heat. James Joule made the association of energy and heat -- weights raised higher (and hence more potential energy) produced more heat when the weights turned paddles in liquid. These results go into the First Law of Thermodynamics which is the conservation of energy.

William Thomson (Lord Kelvin), Rudolf Clausius and Ludwig Boltzmann are associated with The Second Law of Thermodynamics. William Thomson resolved the conservation of energy with some early work by Carnot on engines by distinguishing between energy and "useful" energy. (Like Newton, William Thomson became a "sir" not for his efforts in pure science but for his work involving the telegraph and the laying of the trans-Atlantic line.) Among other things Clausius provided the version of the Second Law that says that energy will not spontaneously flow from low temperature to high. Boltzmann started deriving these results from a microspcopic perspective taking a statistical point of view of all of the atoms or molecules making up the matter.

We discussed that the more general historical backdrop for thermodynamics was the Industrial Revolution. Its development of engines and interest in their efficiency went hand in hand with the development of thermodynamics.

We started to consider the two different views of the same phenomenon: Thermodynamics (the Big View) and Statistical Mechanics (the Small View). The apprearance of "statistical" in the latter suggested it would involve averages, standard deviations, distributions, samples, and other ideas from statistics.

We returned to the consideration of Thermodynamics versus Statistical Mechanics. We introdcued the concept of "state". A "state" is determined by a collection of variables that characterize a system and the "state" is independent of how it was achieved. The state does not depend on the path taken to reach that state. We gave as a counterexample the concept that the frictional force is always against the direction of one's motion, the amount of friction can depend on the "path".

Next we offered up some example of macroscopic variables such as those involved in the (Ideal) Gas Law: Pressure, Volume, Temperature. And we distinguished them from microscopic variables, for instance, the positions, velocities, and accelerations of individual molecules. While it is true that our statistical approach to the latter (microscopic) often end up with the former (macroscopic), the latter approach does go toward explaining the former.

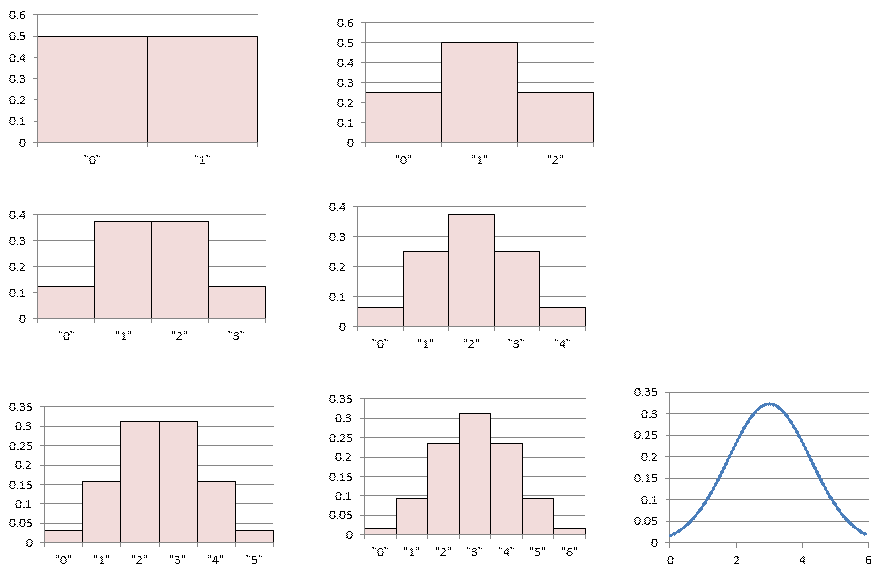
The ideas above led us to the concept of macrostate versus microstate. We took as an example here flipping coins -- the number of heads could be an example of a macroscopic variable whereas noting whether the indivdual coins were heads or tails would be the microstate.

We see from the table above that there is not a 1-to-1 correspondence between macrostates and microstates. There is often an underlying assumption that the microstates are equally probably -- sometimes that some subset of microstates (maybe those with the same energy) are equally likely. If the microsates are equally likely, then the macrostates cannot be. Another version of entropy is that it is proportional to the Log of the number of microstates. We are beginning to define this "disorder" that gets discussed when we speak of entropy. The Second Law of Thermodynamics becomes that a sytem tends toward a macrostate that corresponds to a large number of microstates (i.e. entropy increases).

With that idea about entropy in mind we looked at the Central Limit Theorem, where under certain conditions sets of independent random variables when examined collectively become a normal distribution (aka Bell Curve, aka Gaussian distribution).

Finally we talked about the Thermodynamic approach coming before the Statistical Mechanics approach since the latter relies on a belief in atoms which only came about gradually. (One exception to this general trend was Bernoulli's derivation of Boyle's Law, see pp. 76-79 in Instant Physics (Rothman). So we asked: How do we know there are atoms? One suggestion was microscopes. Microscopes convey that there is structure smaller than what we see with the naked eye, for instance cells, but microscopes did not get down to the atomic level of resolution until the 1980's (Scanning Tunneling Microscope). A lot of the earlier clues about atoms and chemistry came from gases. Studies showed that there just was not air, but different components -- what we know today as Oxygen, Nitrogen and Carbon Dioxide. These were discovered to have particular masses and combine in specific ratios. We also discussed some of the early work in understanding the structure of atoms, in particular Rutherford's experiments that called into question the "plum pudding model."