In order to introduce a mathematical formula (which we didn't quite get to), we started considering the entropy from an Information Theory point of view. We considered a game of "Guess the Number" contrived to make the math simpler. A number would be chosen from between 0 and 127, and the guesser could only ask yes/no questions and must continue asking until he or she was certain of the number. We associated the answer to the yes/no question with the communication of a bit of information -- the basic unit of information.

First we considered the strategy of the guesser. Questions like "Is it 16?" while they have the potential to win the game with a single question are on average poor questions. Questions like "Is the number even?" or "Is the number greater than 63?" are efficient because they eliminate half of the possible answers. Using this "halfing" approach it would require 7 questions to be sure of the number. With the number of possibilities being cut in half with each question, we are down to one possibility in seven guesses.

128 --> 64 --> 32 --> 16 --> 8 --> 4 --> 2 --> 1

The relationship between the original number of possibilities and the number of guesses required is

128 = 2⁷ = 2*2*2*2*2*2*2

Or 7 = Log₂ (128)

Thus selecting a number from between 0 and 127 and conveying to someone either directly or by means on a guessing game corresponds (or at least can correspond) to conveying 7 bits of information. It is said that one round of the game has the capacity of sending 7 bits. The game may seem contrived, but other forms of communication are similar. In writing we have an agreed upon set of letters (or perhaps words) and a "source" communicates with a "receiver" by conveying which the selected item. Similarly in speech we have agreed upon sounds phonemes (or perhaps words) and ....

Next, we considered the strategy of the player selecting the number in the first place. Suppose the selector had a fear of odd numbers, then the guesser could reduce the number of guesses by 1, and hence the selector is only conveying 6 bits of information. Or suppose the selector tends to choose birthdays numbers between 1 and 31. If it is a strong tendency, then the guesser needs only 5 guesses. So the guessing strategy should take into account not just the possibilities but the probabililites of certain guesses.

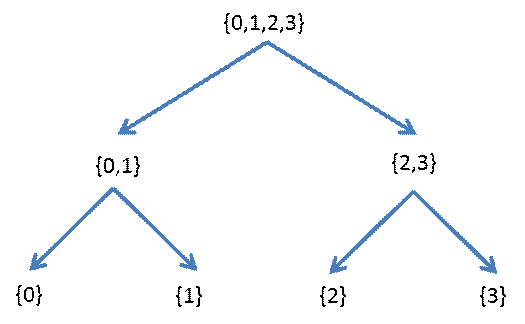
We considered another contrived, simplified scenario of the game. This time there are only four possibilities: 0, 1, 2, and 3, having the following probabilities: 1/2, 1/4, 1/8 and 1/8

Old Approach: Dividing Possibilities	New Approach: Dividing Prababilities

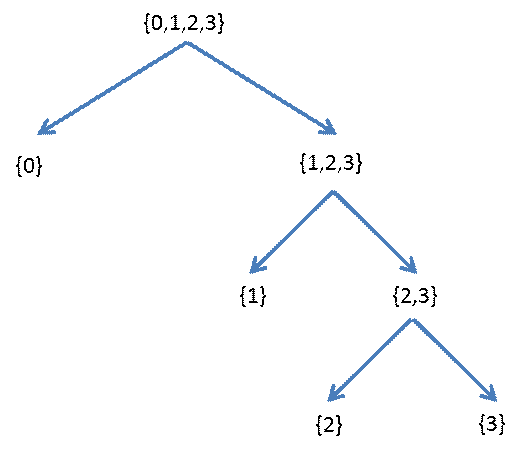The Old Approach guarantees a result in two guesses. The New Approach gets the answer in one guess half the time, in two guesses a quarter of the time, and in three guesses another quarter of the time. So that the expected number of guesses N_guess is

N_guess = (1/2)(1 guess) + (1/4)(2 guesses) + (1/8)(3 guesses) + (1/8)(3 guess) = 1.75 guesses

You Tube: Big Bang Theory Guessing Game