PYL 105

Part I: Incline acceleration

Motion down an incline is a famous experiment that goes back to Galileo. He was one of the first to understand motion with constant acceleration. For instance, he knew that if the object started from rest then its displacement varied like time squared. Later Newton would relate the acceleration of an object to the net force acting on that object. In the absence of friction and air resistance forces, theory says that the acceleration down an incline is given by

a = g sin (θ)

where θ is the angle relative to the horizontal and g is 9.8 m/s², the acceleration due to gravity. We will attempt to verify this result by the following experiment.

• Open up Data Studio, you will find it under Start/Programs/Data Studio/Data Studio - see additional Instructions on the top of the physics lab web site. (The first time someone uses Data Studio in H-053, he/she may have go to Experiment on the menu and select Change Interface and then choose 750.) 
  
  
• Connect the Motion Sensor's yellow plug into Digital Channel 1 and its black plug into Digital Channel 2 of the Pasco Signal Interface on the lab bench.
  
  
• Place the Motion Sensor at the top of the incline as shown in the figure below. It "clips" on. The direction of the sensor can be varied, make sure it is pointed along the track.
  
  
  
  
  
  
• Then on the computer image of the interface, click on Digital Channel 1 and choose Motion Sensor from the list. Set the Sample Rate (found in the middle on the right hand side of the interface's Experiment Setup) to 20 Hz or 25 Hz. What is "sample rate"?
  
  
• Place the cart about 50 cm from the Motion Sensor at the top of the incline. This way the first position is in the appropriate range. (A Motion Sensor cannot measure positions that are too close to it.)
  
  
• Try to coordinate clicking Start (top left) and releasing the cart. You may have to eliminate some initial data if you start recording before the cart is released. Try to make sure that there is is nothing between the cart and sensor (like someone's hand) while data is being taken. Stop the cart and stop taking data. Again there may be data at the end that must be eliminated depending on how well this is coordinated.
  
  
• Double click on "table" in the lower left hand side of Data Studio, then select the type of data (e.g. Position) and the particular Run (e.g. Run 2) that you want the data for.
  
  
  
  
  Then click Edit/Copy on the menu at the top of Data Studio.
  
  
  
  
  Finally open Excel, click in a cell, and then click on Paste under the Home tab.
  
  
  
  
• Following the above directions, copy and paste the position versus time and velocity versus time data over to Excel.
  
  
• We want to analyze only the data when the cart was traveling down the incline without intervention, that is, we do not want data where someone was holding the cart at the beginning nor do we want data where someone is stopping it at the end.
  
  
• In order to estimate the release time or the stop time, make a plot of Velocity versus time
  
   
  
  
  
  The flat region indicates the time before the cart is released, the upward sloping region corresponds to the cart accelerating down the track, and the abrupt downward sloping region is where the cart was stopped (before clicking STOP). The pale yellow rectangle was obtained by holding the mouse over a point in Excel. In the above example we only want data from times approximately 0.4 to 4.6 seconds.
  
  
• If you have never made an XY Scatter graph using Excel or if you need a refresher, follow these instructions (Office 2010). (We will be doing this procedure a lot, learn it!)
  
  
• Using only the times when the cart was "freely" accelerating down the track, make an XY Scatter plot of the position versus time data. Fit the plot to a Polynomial of Order 2.  Extract the acceleration.  How?
  
  
• How would you extract the acceleration from the velocity versus time graph?
  
  
• Ask your instructor whether he or she would like just one or two example graphs or all of them included in your report.
  
  
• Repeat the experiment at this height twice more.  Then repeat the above process for three other incline angles. Do not try to measure the angles directly. Rather measure the height and hypotenuse of the right triangle formed by the track (bottom), block and lab table and use trigonometry.
  
  

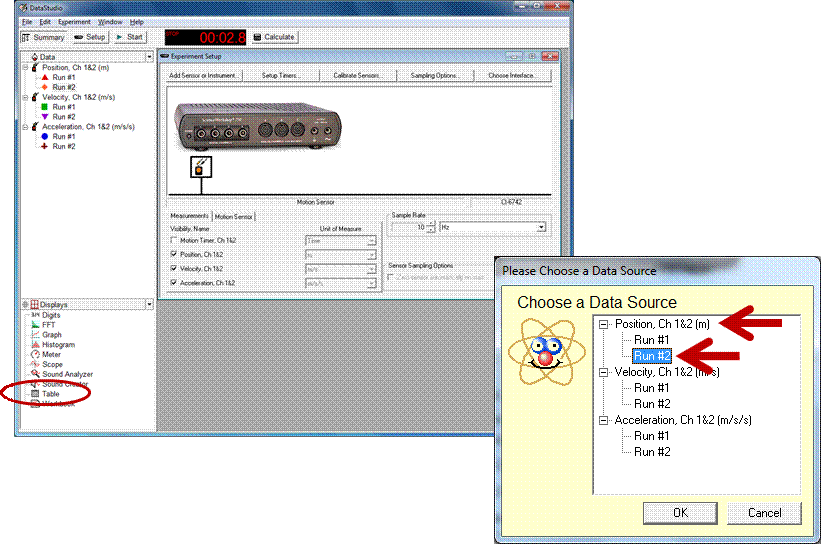
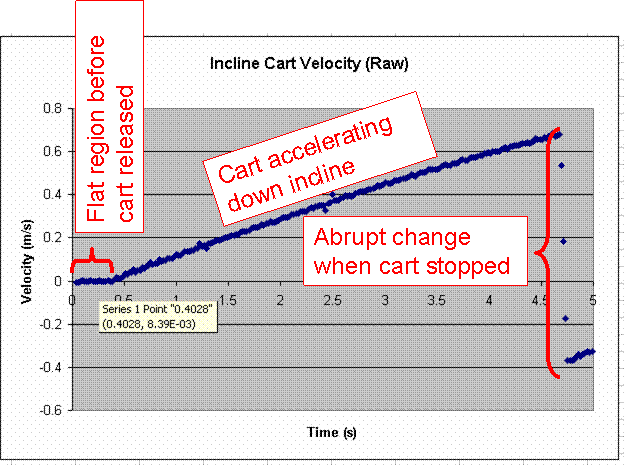
  Incline data
  Length of track (  )
  Height ( )	Angle (degrees)	Theoretical Acceleration ( )	Experimental Acceleration Trial 1(  )	Experimental Acceleration Trial 2(  )	Experimental Acceleration Trial 3(  )	Average Acceleration ( )	Standard Deviation ( )	Percent error bewteen Theoretical and average acceleration

  
  
  
• Excel has a formula for calculating the standard deviation. What information does the standard deviation give about one's data?
  
  
• The percent error is given by:
  
  percent error = ((experimental value - theoretical value)/theoretical value) * 100%
  
  
• Do your experimental results agree with the theory? If not, what might account for the discrepancies?
  
  
• Determine the mass of the cart. For one of your angles, add a metal bar (of known mass) to the cart and repeat the measurements.  Add a second bar (of known mass) to the cart and repeat the measurements again. From the measurements, determine the experimental acceleration.  How?
  
  

  Incline data: Mass variation
  Height (  ):
  Cart Mass (kg) (inc. block)	Experimental Acceleration (m/s2) (from graph)	Theoretical Acceleration (m/s2) (from eq.)	Percent error

  
  
  

You Tube video of dropping objects with different masses on the Moon

Part II: Sketching

Suppose a mass were sliding along a track like the one shown below.

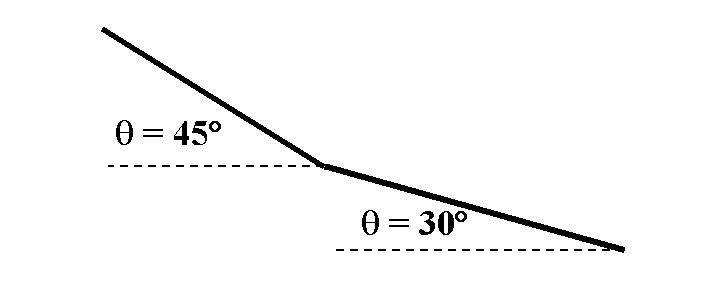
Sketch a graph of what the velocity-versus-time graph would look like. (Assume the track is two meters long and the bend is in the middle.)