PYL 105

Atwood's machine

The figure below shows an Atwood's machine, two unequal masses (m₁ and m₂) connected by a string that passes over a pulley.

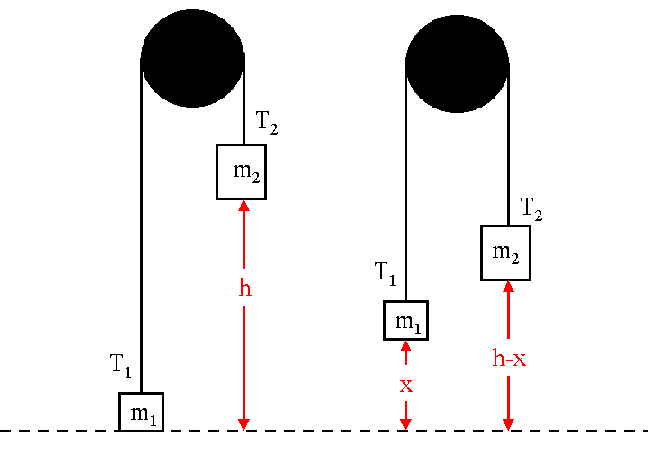
Consider the forces acting on each mass. Assume that the string is massless and does not stretch and that pulley is massless and frictionless. Derive an expression for the acceleration; it should have the form

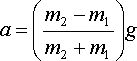
Of course, this is an idealized calculation, and we cannot expect to find this acceleration experimentally. Let us keep the other approximations but drop the frictionless approximation, identifying friction as the cause of any deviation from the ideal acceleration given above. We can then relate the frictional force to the difference between the ideal and experimental accelerations. The ideal force leads to the ideal acceleration

F_ideal = (m₁+m₂)a_ideal

Including the frictional force leads to the experimental acceleration

F_ideal - F_fric = (m₁ + m₂) a_exp

Solve these for F_fric.

We could also adopt an energy approach to this problem. One of the first steps in the energy approach is to determine the "system" for which we are calculating the energy. The "system" could be

• m₁ alone
• m₁ and the earth
• m₁, m₂ and the earth

Determining the system determines whether a force is identified as external or internal and in some cases whether we talk about work or potential energy. For the systems above

• gravity and tension are external
• gravity is internal, tension is external
• gravity and tension are internal

If we consider m₁ and the earth as our system, then the tension is external to the system, and does work on m₁. The work results in a change of energy, both kinetic and gravitational potential energy.

Returning to the frictionless approximation, find an equation relating the work done by T₁ to the change in energy of the m₁-earth system. Assume the mass starts from rest and is displaced a distance x from its initial position. Similarly find an equation relating the work done by T₂ to the change in energy of the m₂-earth system. (They must be included in your report.) Since the tensions are equal in magnitude and the displacements are likewise equal in magnitude, we could eliminate the work done by the tensions to find

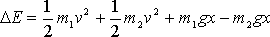
This result is the energy of the m₁-m₂-earth system and ideally ΔE=0, that is, the energy of the m₁-m₂-earth system is conserved. That is, ideally the energy does not change from its initial value which can be taken to be

E₀ = m₂ g h

again assuming that the system starts from rest in the position shown on the left above.

Of course, friction must be brought into the energy approach as well. Just as friction accounted for the deviation from the ideal acceleration in the previous approach, it should also account for any changes in the energy in the latter approach. That is, the work associated with the frictional force (the work done against the frictional force) should equal the observed change in energy.

Measurements

• Find the masses of two sinkers. Use two that are not the same size but are close in size. (The calculations are sensitive to these mass measurements, make them carefully.)
  
  

  m1	m2	h

  
  
• Set up an Atwood's machine, two uneven masses connected by a string that passes over a smart pulley. Set it up at the edge of the bench as shown below so that we can extend our experimental range.
  
  
  
  
  
  
• Set up the interface to use the Smart Pulley.
• Hold the lighter sinker down at the floor level, note the height of the heavier sinker, start recording data and release.
• Copy and paste both the position versus time and velocity versus time data over to Excel. Plot velocity versus time.
• Recall that we do not want all of this data. At some point the lower sinker hits the ground or the higher sinker gets caught in the pulley. Toss out the undesired large-time data.
• Fit a new graph (with bad data thrown away) to a line and extract the experimental acceleration.
• Compare this acceleration to the ideal one and calculate the frictional force
  
  

  aideal     ( )	aexp      ( )	Ffric      ( )

  
  
  
• Note that the times associated with the position data and the times associated with the velocity data are different. The times are staggered.

  

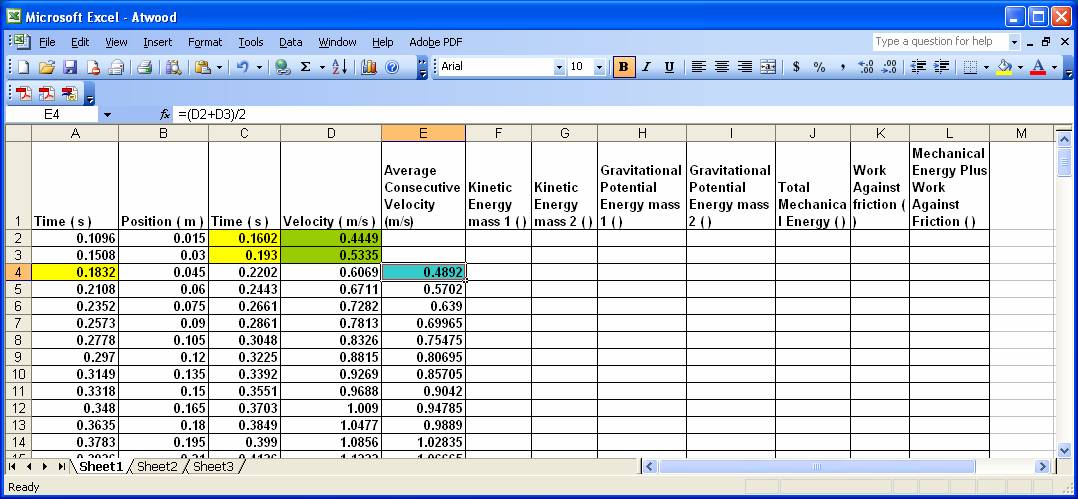
  Calculate the average of two consecutive velocities. For example, you might enter a formula like

  = (D2 + D3)/2

  in cell E4. This will determine the velocities at roughly the times for which we have position data.
• Next use Excel to calculate the terms in the mechanical energy. Use the velocity just obtained.
• kinetic energy of first mass (m₁v²/2)
• kinetic energy of second mass (m₂v²/2)
• gravitational potential energy of first mass (m₁gx)
• gravitational potential energy of second mass (m₂g(h-x))

(In the formulas above m₂ was the heavier mass and started at the higher position.) The corresponding Excel formula could be placed in columns F,G,H and I as shown above.

• In the next column (J), sum these four energy terms. This result is the mechanical energy. Plot mechanical energy versus (position) time.
• If there were no friction this would be a horizontal line (why?)
• How much energy is lost?
• If the change in energy is due solely to the presence of a frictional force, then we can calculate the work done against a constant friction as follows

  W_fric = F_fric x

  Calculate the work done against friction (in column K).

• Add the work done against friction to the mechanical energy. Make a graph which plots simultaneously mechanical energy versus time and mechanical energy plus work done against friction versus time. (Highlight three columns: the time column, the mechanical energy column and the mechanical energy plus work done against friction column, go to Chart Wizard and proceed as usual.) The second curve should be noticeably flatter than the first. Why?
• Is all energy now accounted for?