PYL 105: Centripetal Acceleration

Centripetal Acceleration

A pendulum consists of a weight (known in this context as a bob) on the end of a string (or rigid rod).  The mass experiences two forces: the weight of the bob (directed vertically downward) and the tension (which acts along the string).  

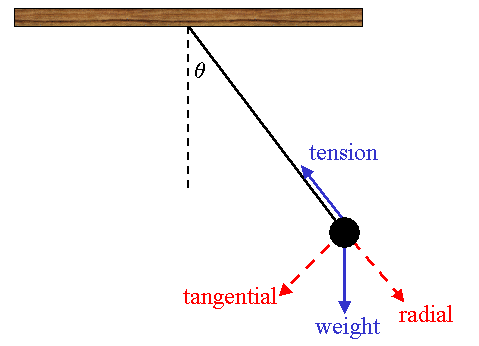
If two forces are not collinear, they cannot possibly cancel out.  For a swinging pendulum there is a net force and hence the pendulum bob accelerates.  Typically one uses a radial-tangential coordinate system (shown in the figure above).  At an arbitrary point in the bob's swing, the net force has both radial and tangential components.  As a result there are two types of acceleration:  centripetal acceleration (which is directed radially) and angular acceleration (which is directed tangentially).

When the pendulum bob is at the lowest point in its swing (when the radial and vertical directions coincide), the forces are collinear, however, the forces have different magnitudes.  Which is bigger? The net force is purely radial and hence the acceleration purely centripetal.   The magnitude of centripetal acceleration is given by

a_centripetal = v²/r

Thus at the bottom of the swing, the net force (Tension - Weight) is responsible for the centripetal acceleration.

Tension - Weight = m a_centripetal

A swinging pendulum is never in equilibrium (i.e. there is always a net force).

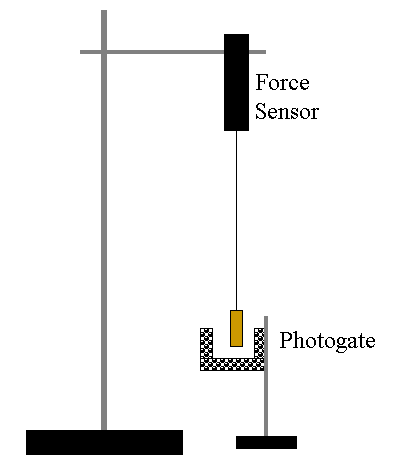
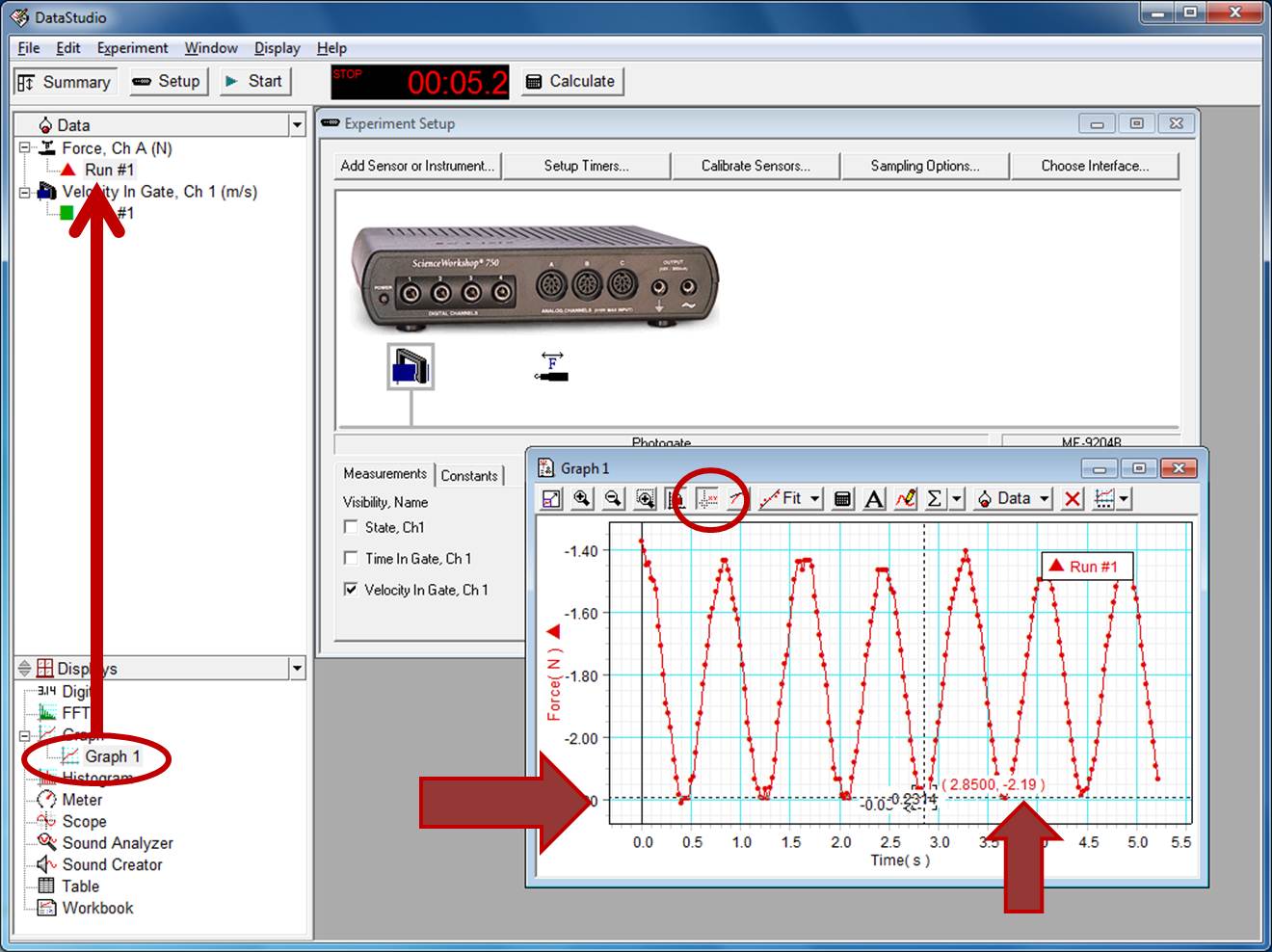
In this lab we will use two measuring devices simultaneously: a Force Sensor to measure the tension and a photogate to measure the speed.  The quantities measured in this lab are somewhat sensitive and require you to take care in making measurements. If your error (disagreement with theory) is greater than 15%, redo the measurement(s).  

Measurements and Analysis

• Measure the diameter and height of a cylindrical weight and record its mass. Use a brass or aluminum (preferably brass) cylinder.
  
  
  

  Cylinder Properties

  Diameter (  )	Height (    )	Mass (   )

  
  
  
• Using a tall ringstand, clamp, Force Sensor, photogate, cylindrical weight and string, make a pendulum set up like the one shown below. The Photogate is a Smart Pulley with the wheel removed.  Please re-assemble the Smart Pulley at the end.
• Inside the photogate U shape, you will see a light/sensor combination. The center of the cylinder's height should be at this level.
  
  
  
  
  
• In Data Studio, drag the analog plug icon into the Analog Channel A icon. Choose Force Sensor from the menu.
• Click on the Sampling Options button (on the left) and change the Periodic Samples (the sampling frequency) to at least 40 Hz.
• Drag the digital plug icon into the Digital Channel 1 icon and choose Photogate from the menu.  On the tabbed section below choose Constants tab and enter the cylinder's diameter (in meters) as the "Flag length".
  
  
  
  
  
• Let the pendulum swing a few times and observe where the pivot point is located.  Measure the length of the pendulum from the vertical center of the bob (cylinder) to the pivot point. Record this length in the table below.
• Hold the cylinder to remove the tension from the string and then Tare the Force Sensor.
• While the cylinder is not swinging, record its weight (the mean reading of the Force sensor) in the table. (Is this value consistent with the mass reading taken above?)
• Start the cylinder swinging through the photogate. It should not be hitting the photogate nor wobbling. Record a few swing's worth of data.
• Drag the graph icon into the Force Analog Channel A. Click the XY cross-hair button at the top of the graph. Place the cross-hairs along the bottom of the Force versus time data  (recall the pendulum's tension is maximal at this point) and read off the force (second number).
  
  
  
  
  
• Drag a table icon into Velocity Digital Channel 1. There should be between four and six readings. Check to make sure that none of the velocities are very different from the rest. Then record the mean velocity in the table above (use the S button).
  
  
  Length (middle of bob to pivot point) =

  Weight (   )	Tension at swing bottom (   )	Net force at swing bottom (   )	Velocity (   )

  
  
  
• Repeat the steps above starting with the taring of the Force Sensor and measuring the weight (always checking for consistency with previous readings).  But each time you start the pendulum, swing it from a different angle. Changing the angle should yield a different velocity. Make measurements for four different angles (yielding various velocities - but avoid small velocities). Try to get as large a range of velocities as possible, i.e. have a small angle and a large angle in your range of angles. (The Force sensors tend to drift, this is why we want to tare them and remeasure the weight each time.)
• Calculate the net force on the pendulum bob when it is at the bottom of its swing (Tension at swing bottom - Weight).
• Plot this  Net force versus velocity. Fit it to a power law.
• Compare your power to the theoretical value. (See centripetal acceleration above.)  If you are not within 15% of the theoretical value, repeat the measurements.
  
  
  

  Fit Power	Theory Power	Percent Difference	Fit Coefficient (  )	Theory Coefficient (  )	Percent Difference

  
  
  
• Extract the coefficient from your fit, enter it above and complete the table. 
• Change the length of the pendulum and repeat the measurements and analysis above. Remember that the length is measured from the center of the bob and that the center of the bob should be at the photosensor's level.
  
  
  Length =

  Weight (   )	Tension at swing bottom (   )	Net force at swing bottom (   )	Velocity (   )

  
  
  

  Fit Power	Theory Power	Percent Difference	Fit Coefficient (  )	Theory Coefficient (  )	Percent Difference

  
  
  
• Repeat with another length. Try to obtain a large range of pendulum lengths (a short, a medium and a long).
  
  
  Length =

  Weight (   )	Tension at swing bottom (   )	Net force at swing bottom (   )	Velocity (   )

  
  
  

  Fit Power	Theory Power	Percent Difference	Fit Coefficient (  )	Theory Coefficient (  )	Percent Difference

  
  
  
• Using the formula from your fits, determine the net force at a velocity of 1 m/s for each of your lengths.
  
  
  

  Pendulum length (  )	Interpolated net force for v = 1 m/s (  )

  
  
  
• Make a plot of (Interpolated) Net force versus length. Fit it to a power law. Compare your power to the theoretical value.
  
  
  

  Fit Power	Theory Power	Percent Difference	Fit Coefficient (  )	Theory Coefficient (  )	Percent Difference

Please re-assemble the Smart Pulley.

Determine the Tension in a 40cm long pendulum when a bob of mass 200g moving at 0.7m/s is 15 degrees from the vertical.
(Hint: determine the radial components of the forces acting on the bob and apply the equation above.)