PYL 105
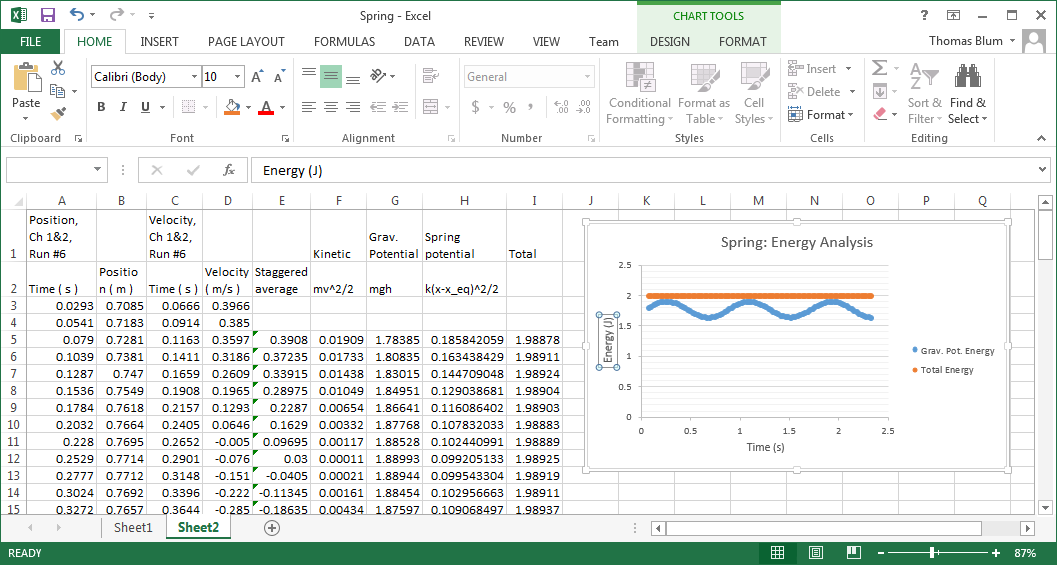
PYL 105





 PYL 105
PYL 105




Much of our previous studies have been about how various quantities change; a velocity is the rate of change of position; an acceleration is the rate of change of velocity; a net force is the cause of an acceleration. However, now we consider a quantity that at least under certain circumstances does not change. The energy of an "isolated" system is conserved meaning that the system's energy does not change as a function of time. Just what is and what isn't a part of the system can be an important decision in considering such problems. Consider the following constant-acceleration equation
v2 = v02 + 2 a ( x - x0)
The above equation does not involve time and using it is essentially an energy analysis. The velocity-squared terms are associated with kinetic energy (the energy associated with an object that is in motion). The acceleration times displacement term can be associated either with the concept of work (which is how an external force in a non-isolated system can change the system's energy) or the concept of potential energy (the energy associated with an arrangement of objects within the system).
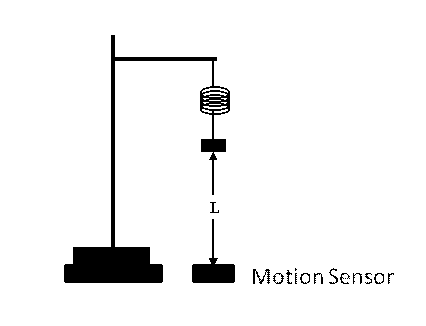
The figure below shows an Atwood's machine, two unequal masses (m1 and m2) connected by a string that passes over a pulley.
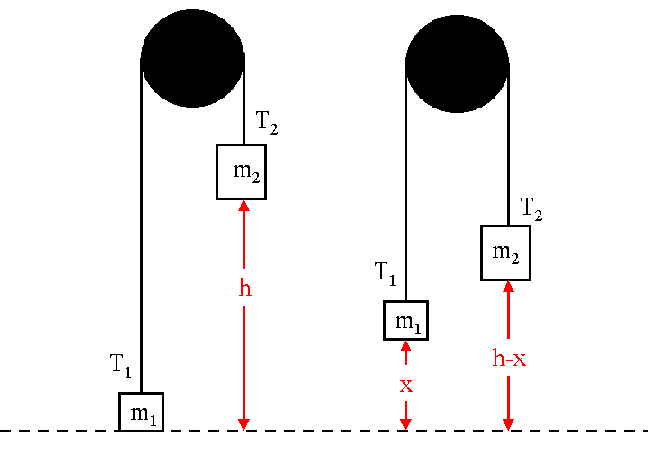
Consider the forces acting on each mass. Assume that the string is massless and does not stretch and that pulley is massless and frictionless. Derive an expression for the acceleration; it should have the form
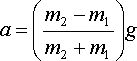
Of course, this is an idealized calculation, and we cannot expect to find this acceleration experimentally. Let us keep the other approximations but drop the frictionless approximation, identifying friction as the cause of any deviation from the ideal acceleration given above. We can then relate the frictional force to the difference between the ideal and experimental accelerations. The ideal force leads to the ideal acceleration
Fideal = (m1+m2)aideal
Including the frictional force leads to the experimental acceleration
Fideal - Ffric = (m1 + m2) aexp
Solve these for Ffric.
We could also adopt an energy approach to this problem. One of the first steps in the energy approach is to determine the "system" for which we are calculating the energy. The "system" could be
Determining the system determines whether a force is identified as external or internal and in some cases whether we talk about work or potential energy. For the systems above
If we adopt the last choice m1, m2, and the earth as our system, then we have kinetic energy of the two blocks and gravitational potential energy of the two blocks. Friction involves the string rubbing against the pulley and the blocks moving through air (and possibly the microscopic motions and arrangemnts of atoms within the blocks) and remains external to our system. Ignoring friction for the moment we would find
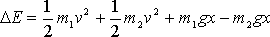
where x is the displacement of the blocks -- one moving with the gravitational force and the other against it. This result is the energy of the m1-m2-earth system and ideally ΔE=0, that is, the energy of the m1-m2-earth system is conserved. That is, ideally the energy does not change from its initial value which can be taken to be
E0 = m2 g h
again assuming that the system starts from rest in the position shown on the left above.
Of course, friction must be brought into the energy approach as well. Just as friction accounted for the deviation from the ideal acceleration in the previous approach, it should also account for any changes in the energy in the latter approach. That is, the work associated with the frictional force (the work done against the frictional force) should equal the observed change in energy.
Measurements
| m1 | m2 | h |

| aideal ( ) |
aexp ( ) |
Ffric ( ) |
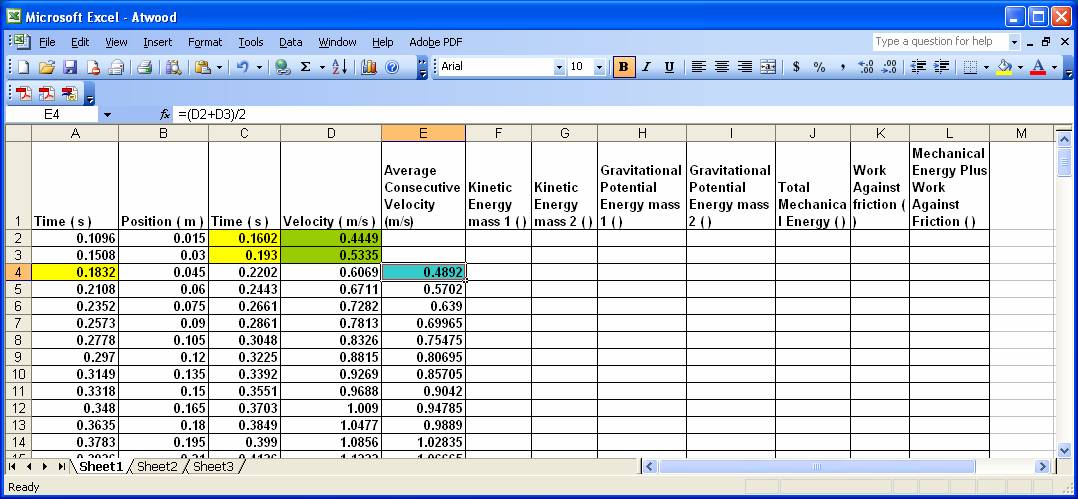
Calculate the average of two consecutive velocities. For example, you might enter a formula like
= (D2 + D3)/2
in cell E4. This will determine the velocities at roughly the times for which we have position data.(In the formulas above m2 was the heavier mass and started at the higher position.) The corresponding Excel formula could be placed in columns F,G,H and I as shown above.
Wfric = Ffric x
Calculate the work done against friction (in column K).
An object is elastic if
Our example of an elastic object will be a spring. You can apply a force that stretches or compresses it. The force that opposes the applied force is called the restoring force. If the restoring force is proportional to the amount of deformation, the object is said to obey Hooke's law.
One can study a spring from a force point of view or from an energy point of view. We will look at a static spring from a force point of view and a moving (kinetic) case from an energy point of view.
F = - k x,
However, L and x are related. What is the relationship? (Note that even with the just the hanger, there is a bit of displacement from the weight of the hanger. You may need to make a graph before you can fill in the displacement column below.)
|
Mass including hanger ( ) |
Distance L from sensor to hanger ( ) |
Displacement x ( ) |
Applied Force
( ) |
| Spring constant ( ) | |
| Equilibrium position ( ) |
Kinetic Case