PYL 105

Hooke's Law

Finding the spring constant

An object is elastic if

• it is deformed when a force is applied, and
• it returns to its origin shape when the force is removed

Our example of an elastic object will be a spring. You can apply a force that stretches or compresses it. The force that opposes the applied force is called the restoring force. If the restoring force is proportional to the amount of deformation, the object is said to obey Hooke's law.

One can study a spring from a force point of view or from an energy point of view.  We will look at a static spring from a force point of view and a moving (kinetic) case from an energy point of view.

Static Case

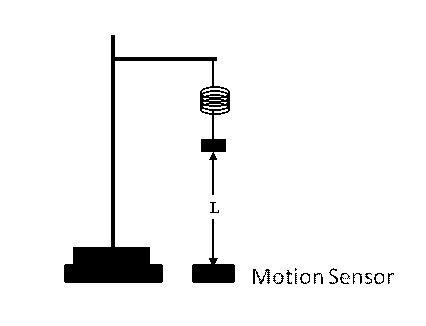
• Using a tall ringstand, clamps, etc. set a spring hanging vertically as shown below. Recall the motion sensor must be at least 0.50 m from the object being measured.

  

• When setting up the motion sensor, select a trigger rate of 40 Hz (put it back to lower setting if the data looks bad -- if the lengths do not match up with a quick meterstick measurement).
• We will apply known weights to the hanger and note the displacement using the motion sensor for consistency with part 2 of the experiment. Record a second or so of position data with the motion sensor and use the Sigma button and copy down the mean position.
• It is not convenient to measure displacement x. What we will measure instead is L, the distance from the bottom of the hanger to a motion sensor on the lab table.
• It is crucial that you understand that this length L is not the displacement x that appears in Hooke's law

  F = - k x,

  However, L and x are related. What is the relationship? (Note that even with the just the hanger, there is a bit of displacement from the weight of the hanger. You may need to make a graph before you can fill in the displacement column below.)

• Add masses to the hanger: 50 g, 100 g, 150 g, 200 g and 250 g and note the distance L.

• Calculate the "applied forces" (the weights, hanger included) and make a plot of Applied Force versus L.
• Fit it to a straight line.
  • What is the interpretation of the slope?
  • What is the interpretation of the x intercept?
  • What is the interpretation of the y intercept?
  (One of these intercepts is the equilibrium position -- the position from which the spring's stretched distance is measured)
  
• Find the x's (displacements) that correspond to your L's and fill in the table above.
• The proportionality constant k is called the spring constant or sometimes a force constant. What is the spring constant for this spring? What are the units (dimensions) of the spring constant?
• What is the meaning of the minus sign in Hooke's law?

Kinetic Case

• Pull one of the larger masses down a few centimeters and release.
• Record the motion.
• Build an Excel spreadsheet similar to the one for the Energy Analysis of the Atwood Machine (previous lab). There should be a number of rows with each row containing: position time, position, velocity time, velocity. Make the adjustments (like last time) so that velocity and position are measured at APPROXIMATELY the same time, calculate all kinetic energy terms, all potential energy terms, total mechanical energy.
• Note that the gravitational potential energy (mgh) can be measured relative to "any" reference point -- use the motion detector's postion, BUT the spring's potential energy kx²/2 must be measured relative to its equilibrium position k(x-x_eq)²/2. (x_eq was found above.)
• Make a plot of position versus time and velocity versus time (2 items on one graph).
• Make a plot of total energy versus time and gravitational potential energy versus time (2 items on one graph)
• The total energy should be a flat line (your graph probably has a small oscillation). One thing that was ignored was the mass of spring. Since the spring has mass and it moves, it has kinetic energy. Also, since the spring has mass that mass is contributing to the stretching the spring as well as the potential energy. Because the spring is not a point object not all of its mass is moving at the same rate (e.g. the top part moves less than the bottom part). Theory predicts that this distribution of mass is equivalent to 1/3 of the spring's mass for kinetic energy but 1/2 of the springs mass for gravitational potential energy and 1/2 for finding the spring equilibrium position.

• Copy your data to a new sheet. Add one half of the mass of the spring to your masses and redetermine the equilibrium position. Add one half of the spring's mass to your gravitational potential energy and 1/3 of the spring's mass to your kinetic energy. Is the resultant total energy any flatter?