Rotational Dynamics

Many of the physical laws previously learned for translational motion (motion in which an object changes location in space) have an analog in rotational motion (motion of an object about an axis). Consider the following analogs:

	Translational	Rotational
Definition of velocity	v = dx / dt	ω = dθ / dt
Definition of acceleration	a = dv / dt	α = dω / dt
Kinematics (with constant acceleration)	v = v₀ + a t x = x₀ + v₀ t + a t² / 2 v² = v₀² + 2 a ( x - x₀)	ω = ω₀ + α t θ = θ₀ + ω₀ t + α t² / 2 ω² = ω₀² + 2 α ( θ - θ₀)
Newton's Second Law	F = m a	Τ = I α
Kinetic Energy	E_kinetic = m v² / 2	E_kinetic = I ω² / 2

where Τ is torque (kg m²/s²), α is angular acceleration (radians/s²), ω is angular velocity (radians/s), and I is moment of inertia (kg m²).

In addition to the analog between translation and rotation, another important set of equations is the relationship between them.

Τ = r × F

x = θ r

v = ω r

a = α r

We could adapt various measurements of translational motion into their rotational analogs. We will consider two basic concepts: torque giving rise to angular acceleration and rotational energy.

Testing Τ = r × F = I α

We will work with the apparatus shown below.

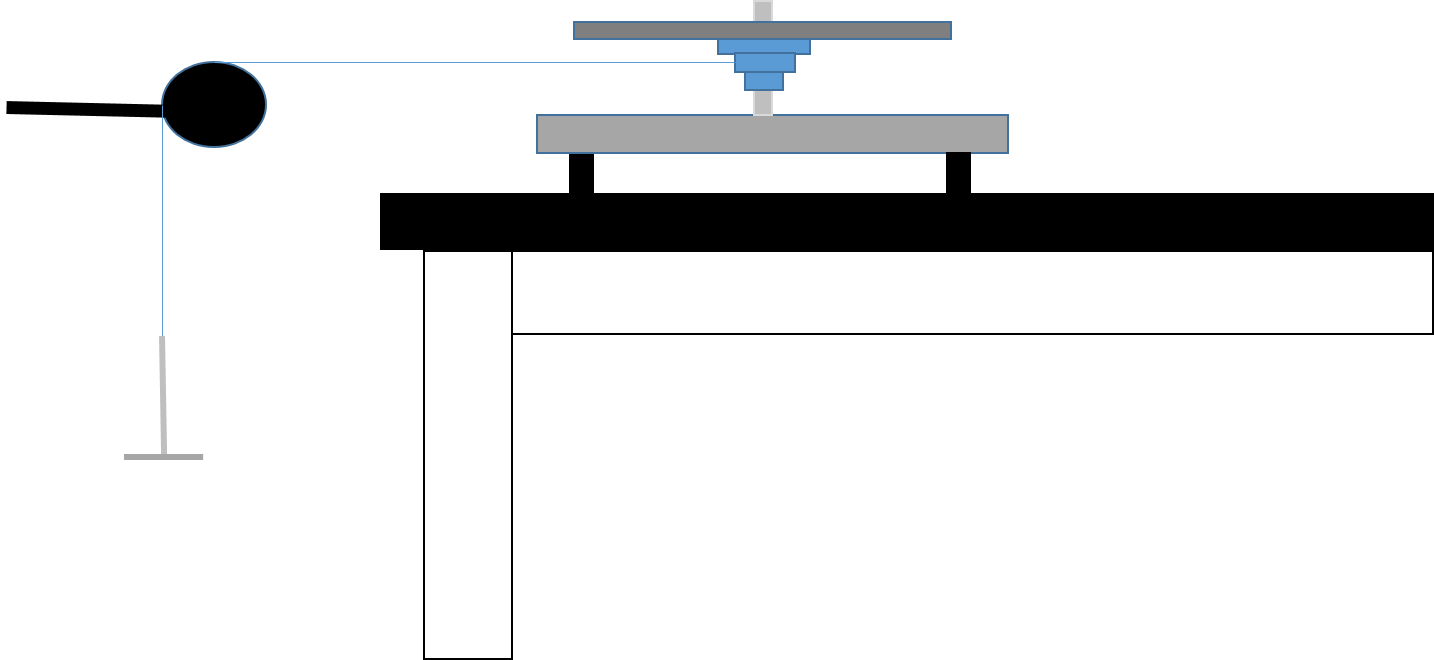
A force diagram on the hanger yields:

m_hang g - Tension = m_hang a

That tension is redirected by the pulley (assumed ideal) and then becomes the force giving rise to the torque. The tension and radius of the pulley should meet at right angles, so that the magnitude of the torque is just the tension times the radius.

Tension r = I α

(m_hang g - m_hang a) r = I α

m_hang g r = I α + m_hang r² α

α = m_hang g r / (I + m_hang r²)

In our experiment the mass and radius of the hanger will be smaller than the mass and radius of the platter, so we will work with the following simplifying approximation

α = m_hang g r / I

Radius variation

Place the main platter on the spindle and insert it into the base.
Attach one end of a string to one of the holes near the center of the main platter.
Attach the other end of the string to a hanger.
Have the string come horizontally from the main platter and pass over a Smart Pulley.
Wind the string around the smallest of the three axes until the hanger is about as high as it will go without interfering with the motion of the pulley. (The axis/spindle radii are 1.50 cm, 2.00 cm and 2.50 cm)
Set up the Smart Pulley in Data Studio to collect velocity versus time data.
From the velocity data obtain the angular velocity data (How?) and make a plot of angular velocity versus time data. Fit it to a straight line and extract the angular acceleration.
Repeat the above data collection and analysis but wind the string around the middle axis.
Repeat the above data collection and analysis but wind the string around the largest axis.

Radius Variation		Weight (including hanger) =
	Radius ( )	Angular acceleration ( )
Small
Medium
Large

Plot angular acceleration versus radius. Fit it to a straight line that goes through the origin (one of the Trenline Options).

Weight variation

Repeat the above data collection and analysis keeping the radius fixed but vary the weight on the hanger. Do not add more than 100 g to the hanger in order for our simplifying approximation to remain valid.
Plot angular acceleration versus weight. Fit it to a straight line that goes through the origin.

Force Variation		Radius ( ) =
	Weight including hanger ( )	Angular acceleration ( )
1.
2.
3.

Moment of Inertia Variation

Repeat the above data collection and analysis keeping the radius and weight both fixed but vary the moment of inertia by adding other apparatus to the main platter.
Plot angular acceleration versus moment of inertia. Fit it to a power law.

Pasco literature values for Moments of inertia
Description	Moment of inertia (kg m²)
Main platter	0.00750
Steel bar	0.00298
Steel ring	0.00246
Auxilliary platter	0.00722

Moment of Inertia Variation		Radius ( ) = Weight ( ) =
	Moment of inertia ( )	Angular acceleration ( )
Main platter only
Main platter with bar
Main platter with ring
Main platter with auxilliary platter

Energy Analysis

Collect data from the Smart Pulley for the position versus time and velocity versus time. (You can use the data from one of your trials above.)
Record the moment of inertia, spindle radius, hanger mass, and hanger initial height.

Moment of inertia ( )
Spindle radius ( )
Mass hanging including hanger ( )
Initial Height of hanger ( )

Copy the position versus time and velocity versus time over to Excel.
As in the Energy lab, calculate the average of two staggered velocities.
From that make a column in which you calculate the angular velocity.
Then calculate the hanger's gravitational potential energy (mg(h-x)), the hanger's kinetic energy (mv²/2), and the platter's kinetic energy (Iω²/2) .
Determine the total mechanical energy and plot total mechanical energy versus time.
Was energy conserved? If not, what was the change in energy? How would you account for the change?

Rotational Dynamics -- Energy Analaysis -- Excel

Calculating Moments of Inertia and comparing to literature values

Collect the following data.

Mass of steel bar ( )
Length of steel bar ( )
Mass of steel ring ( )
Radius of steel ring ( )
Mass of auxilliary platter ( )
Radius of auxilliary platter ( )

From this data estimate the moment of inertia and compare it to the value provided.

	Formula used	Momenta of inertia calculated ( )	Literature value (kg m²)	Percent difference
Steel bar			0.00298
Steel ring			0.00246
Auxilliary platter			0.00722