PYL 105

Rotational Equilibrium

It is easier to open a heavy door when you know where the hinges are. Then you know to apply your force at the opposite end of the door. You also know to push perpendicular to the door's surface. What you are doing here is (for the given force) maximixing your torque.

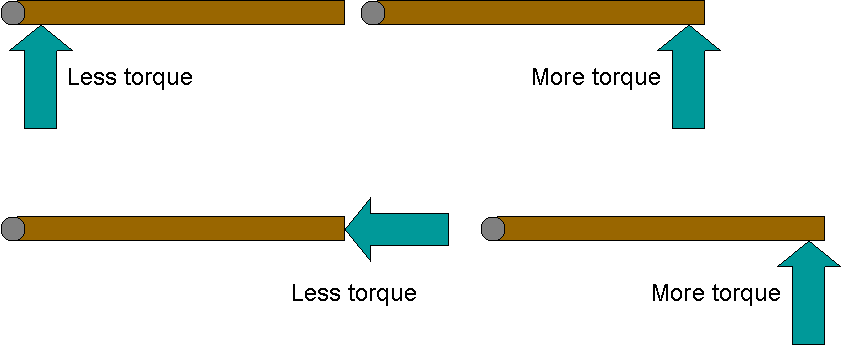
The important factors in determining torque are

• the magnitude of the force applied
• the distance between the axis of rotation and the position where the force is applied
• the angle between the force and the line connecting the axis to the application point

Just as the net force must be zero in order for there to be no acceleration, the net torque must be zero in order for there to be no angular acceleration (rotation). Thus no net torque is another condition for static equilibrium.

Part 1

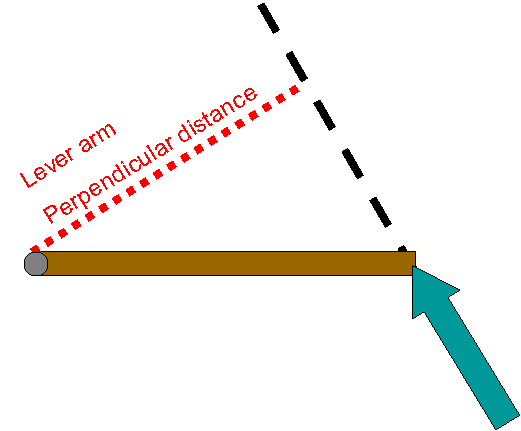
Set up a lever-type system. Recall the following definitions regarding levers.

Fulcrum: the point about which a lever rotates – if the lever is moving this is the point that remains stationary

Lever arm: the (perpendicular) distance between the point where a force (a.k.a. an effort) acts on a lever and the fulcrum

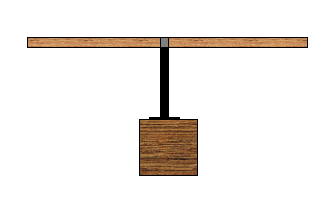
• Obtain the mass of a thick meter stick.
• Obtain the mass of a bracket used to suspend a hanger from the meter stick.
• Attach one bracket near the center of the meter stick and place it on the stand as shown below.

  

• Adjust the position of the bracket until the meterstick is balanced as shown above.
• Record the position (relative to the end of the meterstick) of the center of the bracket.
• This position is the center of mass of the meterstick, x_CM,stick. (It is also its center of gravity since the gravitational field is uniform). The upward force coming from the stand must pass through the center of mass for the stick to be balanced. Is it where you expect?
  
  

  Mstick (  )	x CM,stick (  )

  
  
• Add another bracket and suspend a hanger from it as shown below.

  

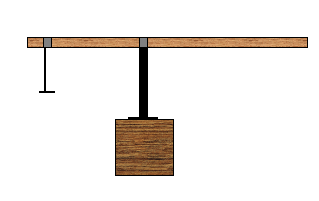
• Adjust the position of the bracket that sits on the stand until the meterstick is balanced as shown above.
• Record the positions (from the end of the meterstick) of the pivot point and the hanger.
  
  

  Pivot Position (  )	Hanger Position (  )

  
  
• From the information above calculate the lever arms R (the perpendicular distance from the axis of rotation to the line of action of the force) associated with the stick's center of mass R_CM and the hanger R_hang. Also record the masses.
  
  

  RCM,stick (   )	Mstick (   )	Rhang (   )	Mhang (  )	Clockwise Torques (   )	Counter- clockwise Torques (   )	Total Torque (   )

  
  
• Calculate the clockwise torque(s) about the axis of rotation – the torques that would if unbalanced make the stick rotate in a clockwise direction.  
• Calculate the counterclockwise torque(s).
• Determine the net torque. (Note that clockwise and couterclockwise torques are considered to be in opposite directions.)
• Repeat the measurements and calculations twice more, changing the mass hanging at least once and the hanger position x_hang,1 at least once.
• Next, add a second hanger to the system, balance it, and record the positions, masses and lever arms.
  
  

  Pivot Position (  )	Hanger 1 Position (  )	Hanger 2 Position (  )

  
  
  

  RCM,stick (   )	Mstick (   )	Rhang,1 (   )	Mhang,1 (  )	Rhang,2 (   )	Mhang,2 (  )	Clockwise Torques (   )	Counter- clockwise Torques (   )	Total Torque (   )

  
  
• Repeat the measurements twice more. At least one time both hanger masses must be on the same side of the stand.

We have been treating all of the mass of the meterstick as acting at one point: its center of mass. From this point of view the weight of the stick leads to just one torque which might be clockwise or counter-clockwise. But part of the stick is to the right of the axis and should cause a clockwise torque, while the rest of the stick is to the left and should cause a counter-clockwise torque. Let us re-analyze the data from the part with one hanger from this new point of view.

• Assume the density of the meterstick is uniform and calculate the mass and center of mass of the right part of the stick (to the right of the axis).
• Similarly calculate the mass and center of mass of the left part of the stick.
  
  

  Rstick,right (   )	Mstick,right (   )	Rstick,left (   )	Mstick,left (   )	Rhang (   )	Mhang (  )	Clockwise Torques (   )	Counter- clockwise Torques (   )	Total Torque (   )

  
  
• Calculate the clockwise, counter-clockwise and net torques.

Part 2: The boom

• Measure the mass of a boom (half a meterstick).
• Attach the boom to a ringstand with the bracket provided.
• Hang a mass from the other end of the meter stick from the other bracket provided.
• Clamp a small pole to the ringstand and attach one end of a force sensor to it.
• Then tie a string from the other end of the spring balance to the top of the bracket from which the mass is hanging. The string should be taut.

  

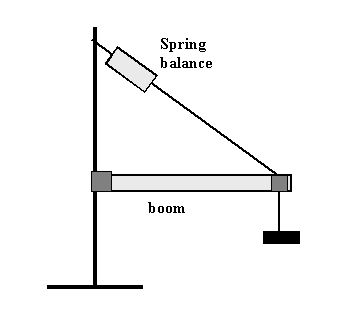
• Measure the tension using the spring balance.
• Measure the anngle between the string and the boom.
  
  

  Rboom (   )	Mboom (   )	Rhang (   )	Mhang (  )	Tension (   )	RTension (   )	Angle

  
  
• Change the mass hanging from the boom and repeat the measurements and calculations.
• Calculate the clockwise, counter-clockwise and net torque about the pivot point.
  
  

  Clockwise Torque (  )	Counter- clockwise Torque (  )	Net Torque (  )

  
  
• Add a second mass between the first mass and the pivot point and make all of the various measurements.
  
  

  Rboom (   )	Mboom (   )	Rhang,1 (   )	Mhang,1 (  )	Rhang,2 (   )	Mhang,2 (  )	Tension (   )	RTension (   )	Angle

  
  
• Calculate the cloclwise, counter-clockwise and net torques.
  
  

  Clockwise Torque (  )	Counter- clockwise Torque (  )	Net Torque (  )

  
  
• In addition calculate the force (both components) exerted on the boom at the pin (pivot point).

Part 3: The ladder calculation

Include as part of your lab, the calculations outlined in torques.doc.