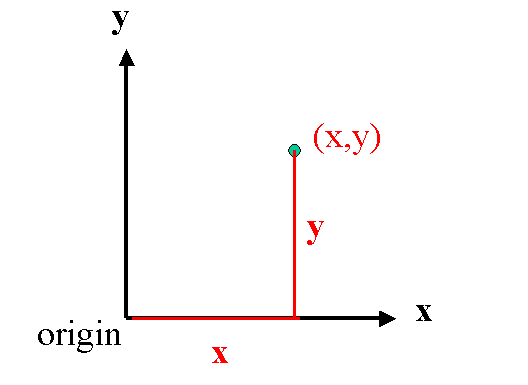PYL 105

Projectile motion

In this lab, we will study projectile motion, which is a special case of two-dimensional motion. In a two-dimensional space, an object's position is given by a pair of numbers (coordinates). There are two standard ways to represent such a position:

• Using Cartesian coordinates
• Using polar coordinates

In Cartesian coordinates there are two orthogonal (at right angles) axes, usually called x and y. Imagine starting at the origin, you can reach a destination position by first moving along the x axis and then along the y axis. The destination point is identified as (x,y), where x is the distance moved along the x axis and y is the distance moved along the y axis. Of course, objects rarely move in this perculiar fashion, it's just a way of thinking about how a position is represented in Cartesian coordinates. The two parts, x and y, are referred as "components."

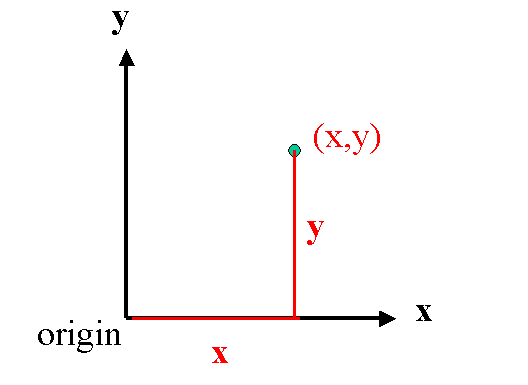
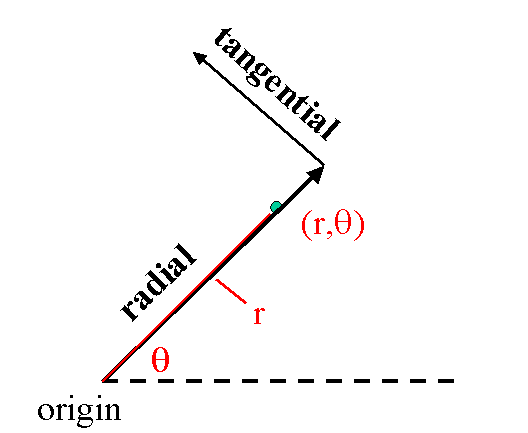
In polar coordinates there are also two orthogonal (perpendicular) axes, the radial and the tangential. The difference is that the polar axes are determined by the point itself. Imagine starting at the origin and moving directly toward the point -- this is the radial direction. The destination point is identified as (r,q), where r is the distance along the radial direction and q is the angle between the fixed axis and the radial direction, measured from the fixed axis to the radial axis in a counter-clockwise fashion. The tangential axis is perpendicular to the radial axis and points in the direction of increasing q.

Projectile motion results when an object is subject to a single force: the constant force of gravity. In this case it is convenient to choose a Cartesian coordinate system with the y axis in the vertical direction (along a line pointing towards the center of the earth) and the x (horizontal) axis perpendicular to the y axis. If one position is represented by a pair of numbers, then the motion, which is a collection of positions, can be represented by a pair of functions

• x(t): the horizontal component of position as a function of time
• y(t): the vertical component of position as a function of time

The orientation of the coordinate system was selected so that the acceleration of the object is solely in one direction, the y direction. Consequently, there is no acceleration in the x or horizontal motion, and the x motion is described by the constant velocity equation

x(t) = x₀ + v_0x t

where x₀ is the horizontal component of the initial position and v_0x is the horizontal component of the initial velocity.

There is a constant acceleration in the vertical direction, and so the vertical motion is described by the constant acceleration equation

y(t) = y₀ + v_0y t - (1/2) g t²

where y₀ is the vertical component of the initial position, v_0y is the vertical component of the initial velocity and g=9.8 m/s², the constant acceleration due to gravity. The minus sign in the equation above is a consequence of implicitly selecting the positive y axis in the upward direction.

Part I: Vertical Launch

Let us begin our measurements with a one-dimensional, purely vertical motion.

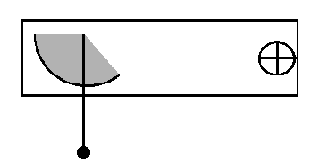
• Aim the launcher (shown below, left) vertically toward a motion sensor that is mounted on a ring stand (shown below, right)
  
  
  
  
  
  
  
• Load the ball into the launcher. There are different settings, i.e. different amounts that the internal spring can be compressed. You must make sure you always choose the same setting (same number of click sounds).
  
  
• Set up the interface/motion sensor.
  
  
• Click Start button and then shoot the launcher.
  
  
• Click Stop after the ball has landed. Ideally, if the motion is purely vertical, the ball should be caught by the launcher.
  
  
• Copy and paste the position versus time data into Excel. The positions are measured relative to the sensor with down as positive direction. To use the y equation above, the measurements need to be relative to the launcher with up as the positive direction. Your position data should have a "flat" portion and a "parabolic" portion. To make the necessary reference and orientation adjustments, insert a column between the time and position column. In the inserted column subtract each position measurement from the flat position measurement. (Explain why this subtraction method places the origin at the launcher).
  
  
• Extract the parabolic part and fit it to a second-order polynomial (use only the time and your inserted columns, not the original position column).
  
  

Polynomial fit eq.




• Take a derivative of that polynomial to find the velocity as a function of time.
  
  

Velocity eq.




• Find the velocity at the beginning of the parabolic part. (Hint: substitute in the appropriate t, it may not be t=0.)
  
  

Part II: Horizontal Launch

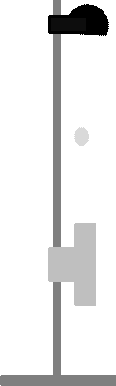
• Your launcher may already have attached the bracket necessary to mount it to a ringstand. If not, remove the nut from the top of the bracket (shown below) and attach the bracket to the nut that is embedded in the launcher.

  

  
  
  
• Notice the plumb line (little string with a weight on the end) and the protractor, they will allow us to determine the angle between the launcher and the horizontal.
  
  
• Fix the launcher to a ring stand so that it is level (zero degrees from the horizontal), as shown below.

  

  
  
  
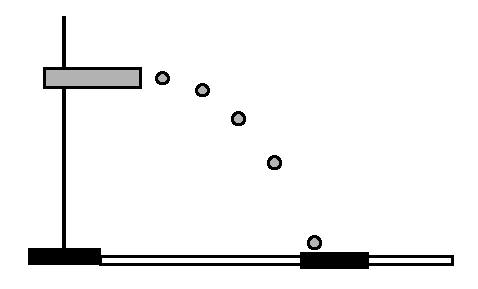
• Take some paper and lay it out in front of the ring stand. You may need a few sheets in order to make sure the various landing positions can be recorded.
  
  
• At the end of the launcher, there is a circle indicating the "launch position" (the initial position) of the projectile. Note the position on the floor or lab table (whichever you are using as the final vertical level of the projectile motion) directly under the center of this circle. (You could use a plumb line, though not the one that comes attached.)
  
  
• Measure h the distance from the bottom of the launch position to the floor.
  
  
• Load the ball into the launcher. (Remember to use the same setting – click sounds – as in Part I).
  
  
• Shoot the ball so that it lands on the paper. Note roughly where it lands and place a piece of carbon paper there. Make sure the ringstand hasn't moved (there's a slight recoil from shooting and/or you might have bumped the ringstand.) Shoot the ball again. Now if you lift the carbon paper, there should be a mark on the paper underneath where the ball landed.
  
  
• Measure x the distance between the point directly below the launch position and the point where the ball landed on the paper.
  
  
• Repeat the above measurement four more times.
  
  
• Change the height and repeat the measurements. Do this for a total of five different heights. There should be at least 50 cm difference between your highest and lowest height. (There should be a total of twenty-five measurements – 5 heights times 5 readings per height – thus far. The column Stand. Dev. is standard deviation, use the Excel function =stdev(range)).
  
  

Analysis.

1. For a given height h, use g=9.8 m/s² for the acceleration due to gravity to calculate the time the ball took in going from the launch position to the floor. Assuming there is no air resistance, the above y equation becomes

   0 = h - g t² / 2

   
   
   
2. Using this time and the average x, calculate the average initial velocity.

   x_av = v_av t

   You should present these results along with your data in the table above.
   
   
3. Calculate the spread in velocities as follows. For a given h, let us take the spread in x (represented by Dx below) to be given by the standard deviation (stdev) of the x's. We could find the spread in the corresponding velocity by calculating each individual velocities and then taking the standard deviation thereof. Or we could apply a bit of calculus

   v = ( x_av ± D x ) / t = v_av ± D x / t,

   D v = D x / t.

   This is a simple example of what is called propagation of errors. Calculate the spread in velocities
   
   

   Propagation of Errors
   Height (     )	Time (     )	Spread in range (     )	Spread in velocity (     )

   
   
   
4. Repeat the calculation of the average speed v_av and its spread for the other heights. The speed of the balls out of the launcher should not depend on the heights of the launcher. Is this what you find? Compare the v_av with the velocity from Part I. (Why compare these velocities?)
   
   

   Velocity Comparison
   Velocity Part I (     )	Average Velocity Part 2 (     )	% difference

   
   
   
   
   
5. Plot h versus (average) x and fit to a power law. Compare the power you find to the theoretical prediction.

   h = (g / 2 v²) x²;

   The predicted power is square (2).

   
   

Part III: Launch at an angle

1. Set up the launcher at a 20° angle with the horizontal such that the bottom of the launch position (circle drawn on end of launcher) is at table-top height, as shown below

   

   
   
   
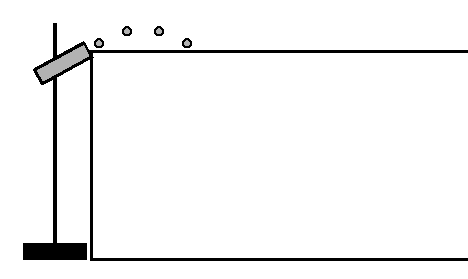
2. Lay out the paper and carbon paper similar to Part II.
   
   
3. Shoot the ball and measure the "range" R, the distance from the launch position to landing position. Repeat twice more.
   
   
4. Repeat the above range measurements for 25°, 30°, ..., 65°, and 70°. Make sure that as you change the angle that the bottom of the launch position (circle drawn on end of launcher) remains at table-top height.
   
   

Analysis

1. Make a table of your experimental ranges as well as the theoretical ranges.

   Projectile Data: Launch from an angle
   Angle (degrees)	Range trial 1 (     )	Range trial 2 (     )	Range trial 3 (     )	Range (     )	Theoretical Range (using Part I v) (     )	Theoretical Range (using Part II v) (     )
   20°
   25°
   30°
   35°
   40°
   45°
   50°
   55°
   60°
   65°
   70°

   The theoretical range R_th is given by

   R_th = v₀² sin ( 2 q ) / g

   Use the initial velocity found in Part I and then the average initial velocity used in Part II. Which gave results closer to those in Part III?

   
   
   
2. For what angle is the theoretical range a maximum? Do your measurements agree with this prediction?