Friction
When an object lies on or moves along a surface, there is a contact force. It is
convenient to break that contact force into two components: one "normal" to the
surface, the other "tangential" to the surface. In fact, the two components are
often discussed as if they are two separate forces. Of course, as we saw
previously in the force lab(s), it makes no difference to its effect whether it is two forces or one force (addition of
vectors).
The force normal to the surface is called the normal force. The normal force
prevents the object from breaking through the surface. Its magnitude exactly
balances all other forces in the normal (perpendicular to the surface)
direction.
The force along the tangential direction is called the frictional force.
Friction behaves slightly differently depending on whether or not the object is
moving relative to the surface.
-
Kinetic: If the object is moving (has a non-zero velocity) relative to the
surface, then friction opposes that motion, i.e., its direction is opposite to
that of the velocity.
-
Static: If an object is not moving relative to
the surface, then the friction opposes any would-be
motion, i.e. its magnitude is equal to and its direction
opposite to the sum of the other tangential forces.
There is a limit to the force that static friction
can successfully oppose. When that limit is exceeded,
motion results.
The frictional force is ultimately due to the interaction
of the object atoms with the surface atoms and vice versa.
The strength (magnitude) of the frictional force might
depend on the following:
-
the number of atoms in contact (microscopic) or the
surface area of contact (macroscopic)
-
the distance between interacting atoms
(microscopic) or the pressure (force per area)
exterted at the surface (macroscopic); the
greater the pressure, the closer the atoms are
squeezed together
-
the kind of atoms (microscopic) or the materials from which the block and surface
are made
In the first part of this course, we usually approximate
objects by point particles. To keep consistent with this
approximation, we assume that the area dependences of the
first two considerations above exactly cancel. One is then
left with the frictional force being proportional to the
force exterted perpendicular to the surface, that is, the
normal force. Any material dependence from the third
consideration will be encoded in the proportionality
constant called the coefficient of friction.
Friction: Finding the coefficient of static friction
In a static situation, the magnitude of the friction force is whatever it has
to be to balance other tangential forces up to some limit, that is,
Ff < ms N,
where N is the magnitude of the normal force and
ms
is called the coefficient
of static friction. The expression
ms N
is the largest the static friction can be. If the
opposing tangential forces exceed it, motion results. The
direction of the frictional force is opposite to the
direction of motion the object would have in the
absence of friction.
Measurements
-
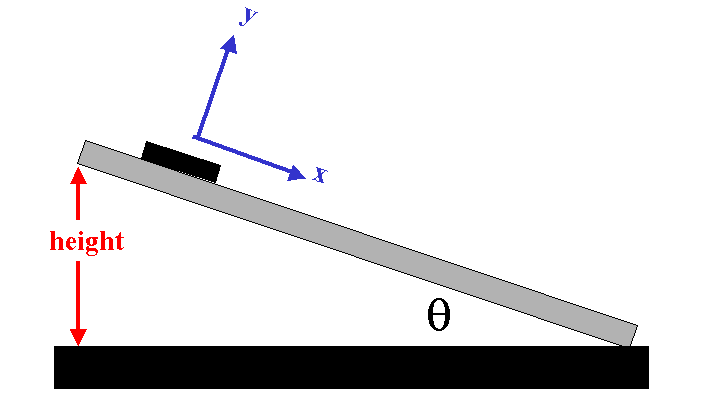
Set up a track as shown below
-
Record the length of the track and masses of the
various blocks.
| Length of track ( ) |
|
| Mass of friction block ( ) |
|
| Mass of heavy metal block ( ) |
|
-
Make sure your track is clean. Sticky parts on the
track will lead to nonuniform coefficients of
friction. Why?
-
Place a friction block (two views of which are shown
below) with the wide wooden surface against the
track. Starting at small angles, increase the angle
until the block first begins to move. Record the
height, then use trigonometry to find the corresponding
angle. (The block just beginning to moves means we are
at the upper limit for static friction.)
-
Repeat this measurement two more times for a total
of three trials for the wide wooden surface of the
friction block.
-
Repeat the measurements for the narrow wooden side,
the wide felt side, and the narrow felt side.
|
Height
trial 1
( ) |
Height
trial 2
( ) |
Height
trial 3
( ) |
Angle
trial 1
( ) |
Angle
trial 2
( ) |
Angle
trial 3
( ) |
ms
trial 1 |
ms
trial 2 |
ms
trial 3 |
ms
Ave |
ms
St. dev. |
| Felt Wide |
|
|
|
|
|
|
|
|
|
|
|
| Felt Narrow |
|
|
|
|
|
|
|
|
|
|
|
| Wood Wide |
|
|
|
|
|
|
|
|
|
|
|
| Wood Narow |
|
|
|
|
|
|
|
|
|
|
|
- Choosing either Felt Wide or Wood Wide, place one of the
heavy metal blocks on top of the friction block and repeat
the measurements (three trials). You may need to tape or some other way to secure the weights onto the friction blocks. Place
a second metal block on the friction block and take another
set of measurements.
|
Height
trial 1
( ) |
Height
trial 2
( ) |
Height
trial 3
( ) |
Angle
trial 1
( ) |
Angle
trial 2
( ) |
Angle
trial 3
( ) |
ms
trial 1 |
ms
trial 2 |
ms
trial 3 |
ms
Ave |
ms
St. dev. |
|
Friction Block Alone |
|
|
|
|
|
|
|
|
|
|
|
|
With One Heavy Block |
|
|
|
|
|
|
|
|
|
|
|
|
With Two Heavy Blocks |
|
|
|
|
|
|
|
|
|
|
|
Analysis
-
Once the block starts moving, does it seem to
travel down the track at a constant velocity? Or
does it appear to be accelerating?
-
In your write-up, draw the set-up above. Draw
all of the forces acting on the block (the weight,
the normal force and the frictional force).
-
Break the forces into their components in the
coordinate system shown above.
-
At an angle just below the one at which the block
began to move, the forces were in equilibrium. Thus
the net force was zero. This should provide you with
two equations (one for the x components, one for
the y components).
-
Using these equations and the form above for the
maximal static friction force, find an expression
for
ms.
(It should depend only on the angle.)
-
Use this expression to find
ms
for your three runs above. Find the standard deviation
as well.
-
What are the dimensions of
ms?
-
Do you observe any dependence on the cofficient of
friction you found on the area of contact?
-
Do you observe any dependence on the material?
-
Do you observe any differences when you add the
heavy block on top?
Friction: Finding the coefficient of kinetic friction
When the object is moving along the surface, we have what is
called kinetic
friction, and in our approximation the formula
is
Ff =
mk N,
(In the case of kinetic friction we have an equation
rather than an inequality; the equation applies provided
the object is moving.)
Measurements
-
Obtain the various masses: friction block, metal
block.
| Mass of friction block ( ) |
|
| Mass on hanger including hanger ( ) |
|
| Mass of metal blocks ( ) |
|
-
Using a universal clamp, secure a Smart Pulley at the
edge of the lab bench.
-
Plug the Smart Pulley into the Digital Channel 1 of
the Data Studio Interface.
-
Start Data Studio, click on the digital plug icon into
the Digital Channel 1 icon, and select Smart
Pulley from the menu. (It is also possible to
make the measurements using a Motion Sensor on the
other end of the track.) Remember to set the Sampling
Rate (Frequency) high enough, e.g. 20 or 50 Hz.
(50 Hz provides more data but is sometimes
problematic.)
-
Tie one end of a string to the friction block and
the other end to a 50-g hanger.
-
Place the two heavy metal blocks on top of the
friction block. Add enough mass to the hanger so that
it sets the friction block into motion. (We want an
acceleration here, but a small one.)
-
Note the distance between the hanger and the floor
so you can stop the friction block before it travels
that distance.
-
Click Start and the release the friction block.
-
Copy the position vs time data and
use Excel to graph it.
-
Fit it a polynomial of order two and extract the
acceleration. (Remember to leave out any data from
the start or end where the "physics changed", e.g.
if it hit the floor. If the data is not reasonably
well fit by a polynomial of order 2, consider
retaking it.)
-
Repeat the process for each of the two wide surfaces
of the friction block being in contact with the track.
|
Acceleration
( ) |
Coefficient of kinetic fricton
( ) |
| Felt Wide |
|
|
| Wood Wide |
|
|
Analysis
Looking at the forces acting on the block and the
hanger and breaking the block forces into components
yields the following three equations:
| Block |
Y comp. |
Nb - mbg = 0 |
| Block |
X comp. |
Tb -
mk
Nb = mb ab |
| Hanger |
Y comp. |
mhg - Th = mhah |
where the subscript b indicates block and the subscript
h indicates hanger. If the string and pulley are
considered massless, then Th=Tb.
Furthermore, if the string does not stretch or break
then ah=ab. Solve the equations
above for
mk.
Enter the value you find for the coefficient of kinetic
friction in the table.
Do you observe any dependence on the material? How do the
kinetic coefficents compare to the static coefficients?


 PYL 105
PYL 105







