

 PYL 105
PYL 105





 PYL 105
PYL 105




Archimedes' principle says: A body wholly or partially immersed in a fluid is buoyed up by a force equal to the weight of the fluid it displaces.
Part 1: Density of water
| Volume ( ) | Mass ( ) |
Part 2: Force as a function of volume displaced

| Slope ( ) from graph |
Slope ( ) from theory |
Percent Difference |
Part 3. The density of brass.
Vcyl = p r2 h
Fweight = rbrass g V
When the cylinder is submerged, there is an additional force, the buoyant force, acting. It is given byFbuoyant = - rwater g V
where the minus sign indicates that the buoyant force is in the up direction while the weight was down. Derive an expression the density of brass rbrass that involves your initial (not submerged) force Fi and final (totally submerged) force Ff from above, but does NOT include volume. In this method you should not use the volume you calculated, but you can use the density of water (rwater = 1000 kg/m3).
| Density of brass Method 1 |
Density of brass Method 2 |
Density of brass Method 3 |
Average |
The nice feature of this last technique is that it does not require any measurement or calculation of the volume. Apply the same technique to measure the density of one of the short hexagonal shaped weights. Also measure the density of one of the longer hexagonal shaped weights.
| Fi (N) | Ff (N) | Density (kg/m3) | |
| Small Hexagon | |||
| Small Hexagon |
Discuss the relative merits of these techniques. What is hydrostatic weighing? What is it used for?
Part 4. Floating
If an object's density is less than water, it will float. That is, it will be positioned at the surface of the water with only some of its volume below the surface. If the object is in equilibrium then its weight must be balanced by the buoyant force (assuming no other forces are acting).
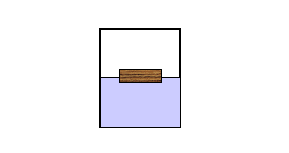
| Length (m) | Width (m) | Height (m) | submerged Height (m) |
Weight of block (N) |
Weight of water displaced (N) |
Percent Difference |
One possible difficulty with this measurement is in determining the amount of the block that is below the surface. This is because fluids do not meet the surface of the block at a right angle. Typically the fluid-block interface will look roughly like one of the pictures below.
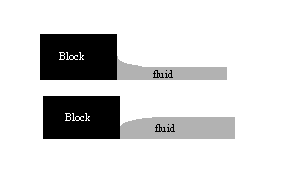
We say in the case on the top that the water "wets" the surface. In this case, if you measured the length of wetness to obtain the "submerged height," you would tend to overestimate the submerged volume. Those of you who have had chemistry may have seen/discussed this phenomenon in connection with the meniscus. Comparing the actual weight of the block to the calculated weight of the water displaced, do you think you underestimated or overestimated the displaced volume?
