Wednesday:
We derived Snell's Law which describes the bending of a light beam as it crosses a surface between
two media having different indices of refraction, n1 and n2. We imagined a beam of
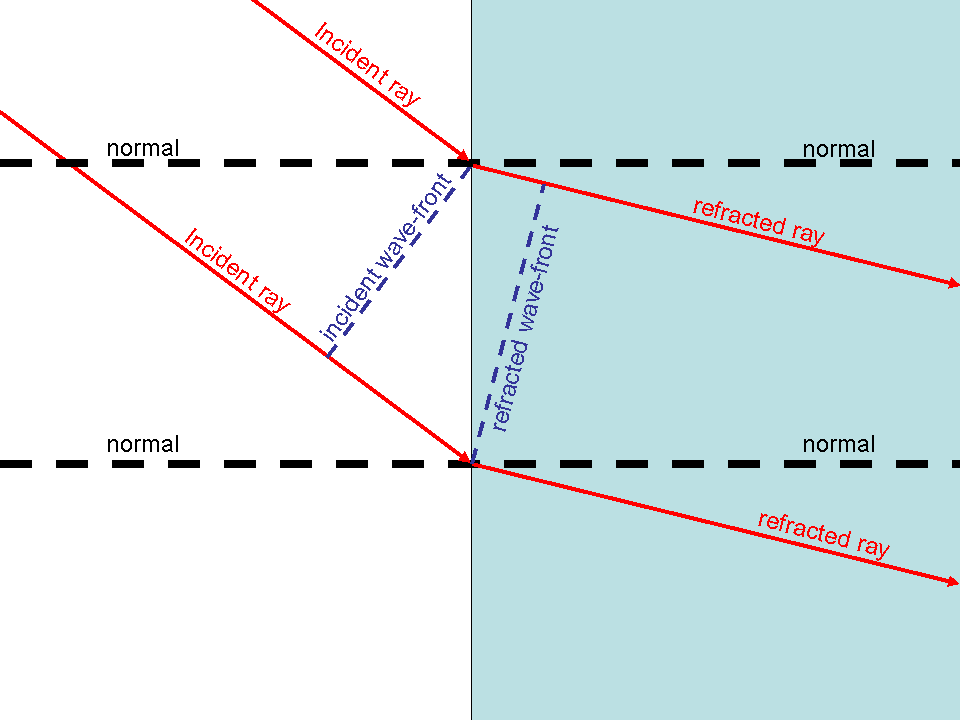
light (of some thickness) and described it using rays which are along the beam's direction of
motion and wave-fronts which are perpendicular. In particular we considered wave-fronts
at the
wave crests (maxima) and thus wave-fronts were separated by the wavelength λ.
Because the incident ray is not normal to the surface, the entire wave-front
does not hit the surface simultaneously. Below we show two consecutive wave-fronts – one
in medium 1 and the other in medium 2.
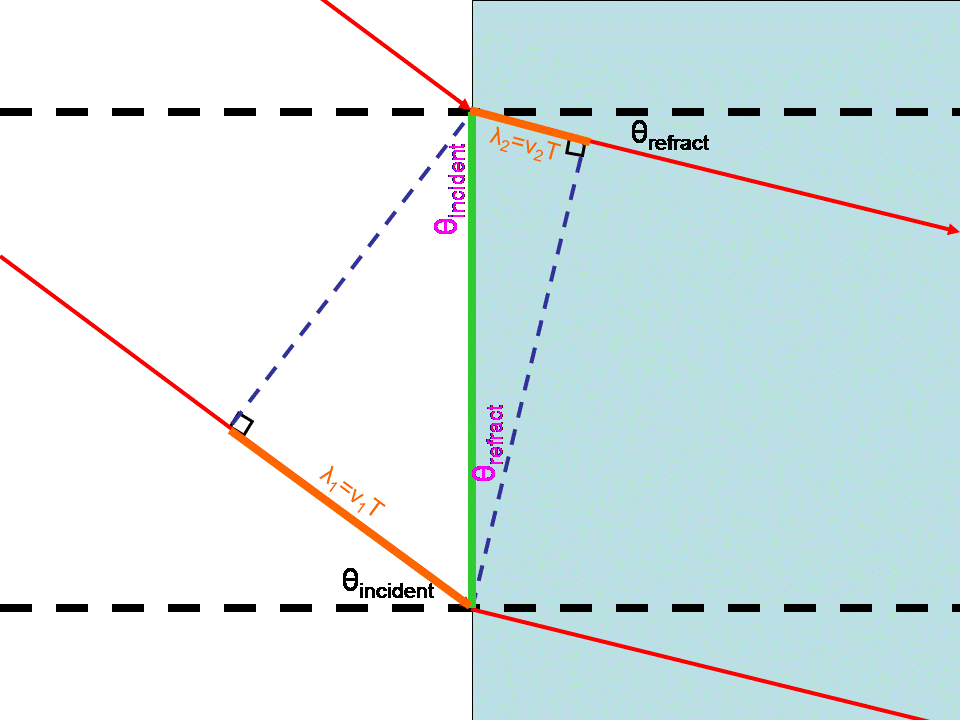
We focused in on the two triangles toward the middle that had a shared side along
the surface (shown below in green), which happens to be the hypotenuse of each.
We used geometry to show that the angle between the ray and the normal was the same
as the angle between the wave-front and the surface. Because the wave-fronts represented
consecutive maxima, they were separated by wavelengths. The wavelengths (shown in
orange below) were given by the speed in the material multiplied by the period, which
is the same for each. (Afterall the reflected wave is a response to the incident
wave, and response tend to have the same frequency as their "driving" frequency.
hyp = λ1 / sin(θincident)
= λ2 / sin(θrefracted)
v1 / sin(θincident)
= v2 / sin(θrefracted)
c / n1 sin(θincident)
= c / n2 sin(θrefracted)
n1 sin(θincident)
= n2 sin(θrefracted)
The above equation is known as Snell's Law.
We argued that a very similar derivation could be done for the reflected beam – with the important
distinction that the medium for the incident and reflected beams is the same. This discussion led
us to the conclusion known as The Law of Reflection
θincident = θreflected