PYL 106: Diffraction and Interference

Interference and Diffraction of light

Just as we had superposition of waves on a string and sound waves, we have superposition of light waves. We will send laser light (you should discuss in your report why we are using lasers) through a pattern of slits. According to Huygens' Principle, the light that passes through these slits can be thought of as a new source. So now we have multiple sources of light, just as we had multiple sources of sound waves (speakers) in the superposition of sound lab. The waves from these sources will interfere, sometimes constructively, sometimes destructively, yielding bright and dark spots respectively.

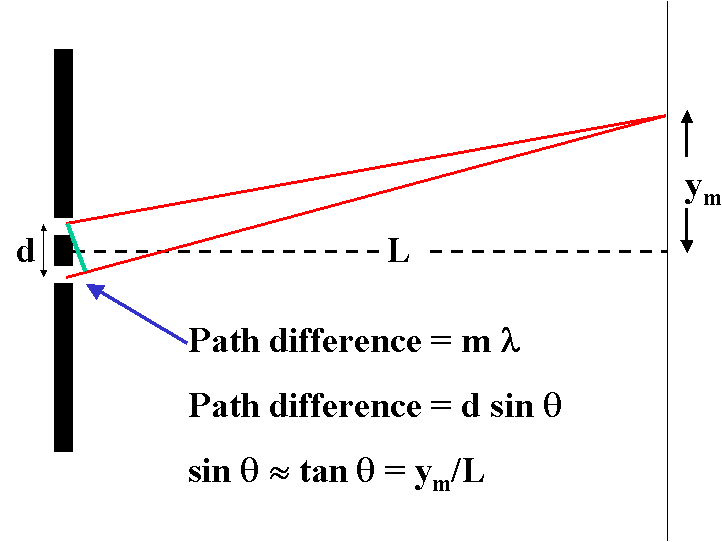
The centers of the bright spots should be at places of constructive interference, i.e. where the path difference is an integral multiple of the wavelength. After some analysis and approximations we are led to a relatively simple formula

y_m = m λ L / d

where y_m is the distance between the center spot and the m^th bright spot from it, m is an integer (1, 2, 3 ...), λ is the wavelength of the light, L is the distance between the slit source and the screen where the spots are observed, and d is the distance between the slits.

The above equation is a variation of

d sin(θ) = m λ

where sin(θ) is approximated by y/L.

Part I. Double Slit: Vary Distance Between Slits

• Attach a multi-slit set (which is comprised of two parts shown below)
  
  
  
  
  
  and a diode laser to an optics bench as shown below.
  
  
  
  
  
  
• Plug in the laser, turn it on, and adjust the horizontal and vertical settings so that the beam goes through the slit(s) in the center of the multi-slit set and ends on the screen (piece of paper taped to a cabinet or wall across the room).
• Set the multi-set to the a=0.04 mm, d=0.5 mm double-slit setting (a is slit the thickness, d is the distance between slit centers).
• Note the wavelength of light (if it's not stamped on the laser, look up the wavelength of red light).
• Record the distance L from the multi-slit set to the screen.
• Observe the interference pattern. Record y – the distance between the middles of the center spot and an adjacent bright spot.
• Measure the distance between two other adjacent spots (neither of which is the center spot). How does it compare to y?
• Choose the a=0.04 mm, d=0.25 mm setting and repeat your measurements.
• Choose the a=0.04 mm, d=0.125 mm setting (the double slit, n=2, setting under the multiple slit settings) and repeat measurements.
  
  

  λ =

  L =

  
  
  
  Slit-Width Variation

  a      (mm)	d      (mm)	y1 (center)  (   )	y (not center)  (    )
  0.040	0.500
  0.040	0.250
  0.040	0.125

  
  
  

Analysis

1. Plot y versus d and fit it to a power law. Do your results agree with the formula above?

Part II. Double Slit: Vary Distance Between Set and Screen

1. Put the multi-set on the a=0.04 mm, d=0.125 mm double-slit setting.
2. Change L, the distance from multi-slit set to screen, record it and remeasure y, the distance between adjacent spots.  (If the spots are evenly spaced, you can take the distance to the next-next spot and divide by two, etc.) 
3. Change L three more times, repeating the measurements. Make sure your L's cover a substantial range. Your largest should be many meters.
   

Analysis

1. Plot y versus L and fit it to a power law. Do your results agree with the formula above?
2. Calculate the theoretical y's from the formula and compare them to your experimental values.

Warning: Be careful with units in your calculations.

Part III. Multiple slits

1. Look at the patterns from the 3-, 4- and 5-slit settings. You should included a drawing of them, a description of them, or a photo of them in your report. They should be distinct from the 2-slit patterns considered above. Show your pattern to the instructor.
2. In the patterns, what is different from the two-slit case? What is the same?
3. Account for the change in the pattern by making a plot from 0 to 2π in Excel of the following functions  
   
   

   slit	Function
   2.	1 + cos (φ)
   3.	1 + cos (φ) + cos (2 φ)
   4.	1 + cos (φ) + cos (2 φ) + cos (3 φ)
   5.	1 + cos (φ) + cos (2 φ) + cos (3 φ)+ cos (4 φ)

   
   
   where φ correspond to the phase difference between two adjacent slits. (Note that the brightest spots occur when the adjacent slits that have a phase difference of 2π.)
4. The "2π spots" (i.e. the main ones as opposed to the little in-between ones) decrease in intensity (brightness) as one moves away from the center spot. In the 5-slit pattern you should observe a "2π spot" that has an "out-of-order" faintness. To which integer m does it correspond? Does this make sense? Explain. You may want to see http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/mulslid.html where they show a double-slit pattern formed within the "envelope" of the single-slit diffraction.  Where do you expect the single-slit envelope to have its minimum?

Part IV. Ronchi grating

1. Now replace the slit setting with a Ronchi ruling which has slit after slit after slit.
2. Record its code (color and number of dots, e.g. one red dot or two black dots). This code must appear in your report.
3. Determine d, the distance between slits, for the Ronchi ruling from the pattern you observe.
4. Choose a different Ronchi ruling and repeat.