This lab has two parts. The first part is on Kirchhoff's laws. The second part is on RC circuits.

Kirchhoff's Rules

If two resistors are in series, then the two resistors can be added to find the equivalent resistance. If two resitors are in parallel, then the two resistors can be added reciprocally to find the equivalent resistance. However, there are arrangements of resistors which are neither in series nor in parallel. In such cases one can apply Kirchhoff's rules. One rule concerns nodes – places where wires meet. It says the currents coming into the nodes must equal the currents leaving the nodes. If this were not true, a charge (it might be positive or it might be negative) would accumulate at the node. But nodes are made from conducting materials, and charges do not accumulate inside conductors (outside perhaps, but not inside). Another rule concerns loops. It says that as one traces through a closed loop that the gains in the voltage level must equal the losses in the voltage level. An gravitation analogy in which the level is height would be that one can walk around a building changing one's height using stairs, ramps, elevators, but if one comes full circle back to one's starting point, then any increases in height are balanced by decreases in height.

Charging and discharging a capacitor: RC circuits

When you connect an uncharged capacitor and a resistor in series to a battery, the voltage drop is initially all across the resistor. The voltage drop across a capacitor is proportional to its charge, and it is uncharged at the beginning. But charge starts to build up on the capacitor, so some voltage is dropped across the capacitor now. With less voltage being dropped across the resistor, the current drops off. With less current, the rate at which charge goes onto the capacitor decreases. The charge continues to build up, but the rate of the build up continues to decrease. In mathematical language, the charge as a function of time Q(t) increases but its slope decreases.

Theory says the charge obeys

where t is the time, C is the capacitance, V_S is the saturation voltage which in this case is equal to the voltage across the battery, and τ=RC, a time constant. The corresponding voltage across the capacitor is

Now consider the case of a charged capacitor, a resistor and no battery. With no battery to "push" the charges around, the opposite charges on the capacitor plates would prefer to be together. They must pass through the resistor before they can reunite. With all those like charges on one plate, there is a strong incentive for charges to leave the plate. However, as charges leave the plate, this incentive decreases, thus the rate at which charges leave decreases as well. In mathematical language, this time the charge as a function of time Q(t) decreases and its slope decreases.

Theory says the charge obeys

where t is the time, Q₀ is whatever charge we happen to start with, and τ=RC is the same time constant as above. The corresponding voltage across the capacitor is

where V₀ is the initial voltage.

EXPERIMENT 1

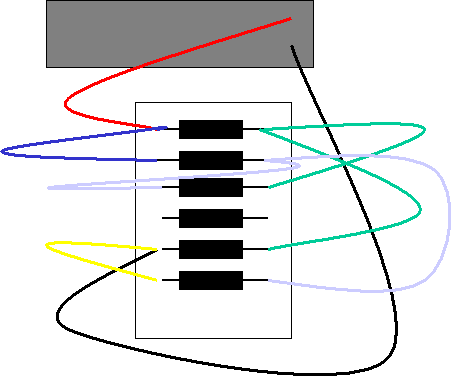
• Set up the Simpson multimeter as an ohmmeter. (If there are three holes on the left-hand side of your multimeter, make sure the red lead is plugged into the hole marked V-Ω and that the DC (direct current) and kΩ button are depressed.
• Press the 20 on the lower front.
• Insert one needle in each hole adjacent to the resistor, allow some time for the reading to settle down, and record the resistance below.
• Measure the resistances R_A, R_B, R_C, R_E, R_F and record them in the table below. (Resistances are measured when the resistor is not connected to a circuit.)
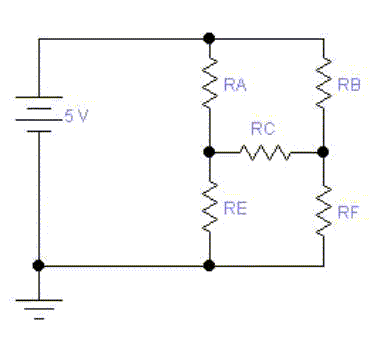
• Next, connect the resitors in a circuit like that shown below
  
  
  
  
  
  Your version may look more like this
  
  
  
  
  
  Look in the above circuit for resistors that are in series (resistors are in series if the current passing through the first is the same, no more no less, as that passing through the second). There are none! Look in the above circuit for resistors that are in parallel (resistors are in parallel if the "tops" and "bottoms" of the resistors are connected by wire and only wire). There are none. The analysis of such circuits requires Kirchhoff's rules.
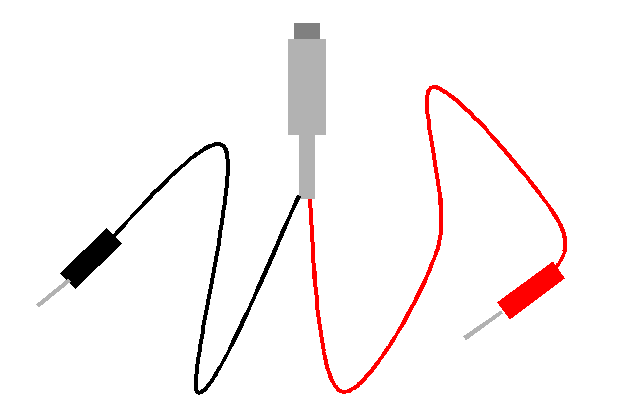
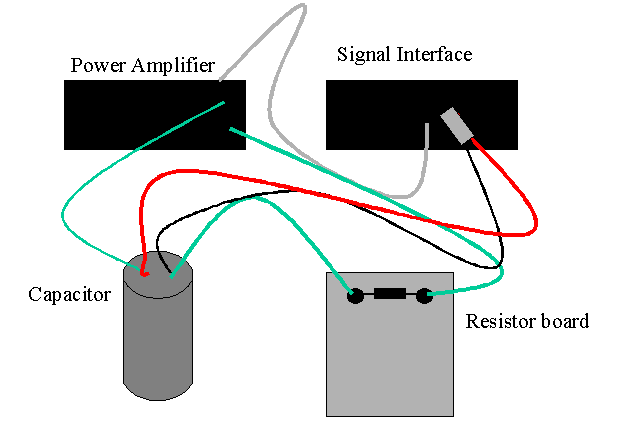
• Set up the power amplifier as a DC power supply, connect it to Data Studio, etc. Set it to a volatge difference of 5 volts.
• Set up the Simpson multimeter as a voltmeter and measure the voltage across the resistors and enter them in the table below.
  
  
  Data from Kirchhoff Experiment

  	Resistance (    )	Voltage (    )	Current From Experiment (use Ohm's Law) (    )	Current From Theory (use Kirchhoff's rules) (    )	Percent     Error
  RA
  RB
  RC
  RE
  RF

  
  
• Obtain the experimental current from your resistances and voltages using Ohm's law I=V/R and enter them into the table above.
• Solve Kirchhoff's laws for the currents in your circuit and enter them into the table above. Include the solution in your report. (Collect the data for the second part of the experiment before performing this analysis.) One way to solve Kirchhoff's equations is by using a matrix approach, for an explanation of this approach, see this slide show on Kirchhoff. Here is a matrix equation spreadsheet like the one discussed in the slide show.

EXPERIMENT 2

Part I: Charging:

• Connect your interface to a power amplifier and set it up as a DC voltage source.
• Connect a voltage sensor (shown below) to analog channel B.
  
  
  
  
  
  
• Then in Data Studio click on the analog plug icon into the analog channel B icon and choose "voltage sensor." Drag a graph into analog channel B so we can see the data as it comes in.
• Set the voltage to 5.00 V.
• Make a circuit with resistor R_A and a capacitor in series (have the power amplifier "off"). Your capacitor should be discharged. Diagrammatically this circuit is represented by
  
  
  
  
• Put the leads of the voltage sensor across the capacitor. Your circuit will look something like the following
  
  
  
  
  
  The green wire represents the RC circuit (resistor and capacitor in series), while the black and red wires represent the voltage probe.
• Click Start to turn on the voltage and start recording data.
• You should see the voltage increase and "saturate" at 5.00 V. When it is very close to 5.00 V, stop recording, disconnect the capacitor and then turn off the signal generator. You must disconnect first so that the capacitor will have a charge left on it!
• Table the data, click the clock, copy and paste the data over into Excel.
• The charging capacitor data should be described by the equation
  
  
  V(t) = V_S [1 - exp( - t / τ ) ],
  
  
  where V_S is the saturation voltage, τ is a characteristic time, and where it is assumed that t=0 is when we switched on the voltage supply.
• If you started recording before switching on the signal generator, you must adjust the time. (Ask for help if this is the case with your data.)
• Plot Voltage vs Time
• At this stage follow these instructions for fitting the data.
  
  
  Charging R_A

  VS (   )
  τ (   )

  
  
  

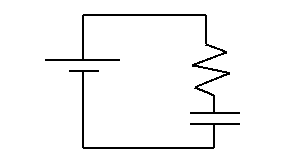
• With the voltage sensor across the now charged capacitor, begin recording a new set of data.
• Connect the capacitor to resistor R_A (no power supply).
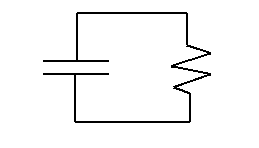
• The voltage should start close to 5.00 V and decay to zero. Diagrammatically the circuit looks like the following
  
  
  
  
  
  
• Copy and paste the data (times and voltages) into Excel.
• For this case you can use the exponential option in Add trendline. Compare the τ's.
  
  
  Discharging R_A

  V0 (   )
  τ (   )

  
  
  

Part II

• Repeat the charging part of the above measurements with resistor R_B.
• Then repeat the discharging part of the above measurements with the combination of R_A and R_B in series.
• Do the plotting as above and compare τ's.
• Does the result agree with theory?
  
  
  Charging R_B

  VS (   )
  τ (   )

  
  
  
  Discharging R_A and R_B

  V0 (   )
  τ (   )
  Theory τ(   )
  Percent Error

  
  
  

Part III

• Get the measurements of the resistances R_A and R_B from the Kirchhoff part of the lab.
• Use your results to extract the capacitance. Note this is the first time we have a capacitance as opposed to a ratio of capacitances.

  RA (   )
  RB (   )
  C (   )

Include in your report:

• What is your best estimate of the time constant if the resistors in the part-II discharging had been in parallel?
• What would happen to the time constant (increase or decrease) if we replaced the single capacitor with the combination of it and a second capacitor in series? Why?
• What would happen to the time constant (increase or decrease) if we replaced the single capacitor with the combination of it and a second capacitor in parallel? Why?