

 PYL 106
PYL 106 





 PYL 106
PYL 106 



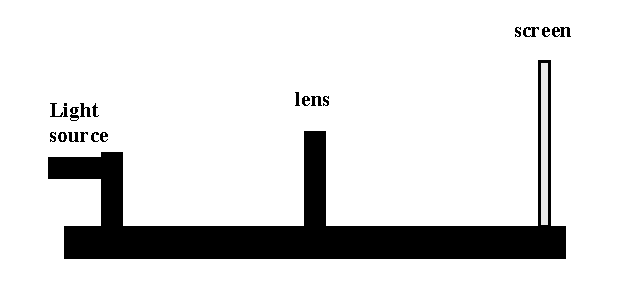
One use of refraction, the bending of light rays, is lenses. There are two surfaces (air-to-medium and medium-to-air). If the surfaces are approximately spherical and close together, one has what is called a "thin lens". The results of the bending can be simplified into an equation called the thin lens equation
1/p + 1/q = 1/f.
In your report, you should tell me the meaning of each of the quantities appearing in this equation. The variables are distances from the lens to certain points. So in addition to identifying these distances, you should answer the questions: What is "the image"? What is the "focal point"?
|
p ( ) |
q ( ) |
yo ( ) |
yi ( ) |
q / p |
yi/ yo |
f ( ) |
Repeat the measurements above for the lens marked +100mm.
|
p ( ) |
q ( ) |
yo ( ) |
yi ( ) |
q / p |
yi/ yo |
f ( ) |
|
p ( ) |
f ( ) |
q ( ) |
q / p |
# of segments
through lens |
# of segments
over lens |
Estimated
Magnification |
Image
inverted |
Note that the image above is very rounded (distorted). One can improve this situation by addding a second lens.
|
p1 ( ) |
f1 ( ) |
q1 ( ) |
D ( ) |
p2 ( ) |
f2 ( ) |
q2 ( ) |
| q1/ p1 | q2/ p2 | (q1/ p1)(q2/ p2) |
# of segments
through lens |
# of segments
over lens |
Estimated
Magnification |
Image
inverted |
