The Pendulum

A mass hanging from a string or attached to a rigid rod, i.e. a pendulum, is another example of a system which exhibits periodic motion. (In such a case, the mass is known as a bob.) The equilibrium position is when the string or rod hangs vertically. If the pendulum is not in this position, there is a restoring force. One of the quantities studied for a pendulum is the angle between the string and the vertical. Remember the angles we are talking about will be measured in radians.

Recall that the period T is the time taken before the motion starts repeating itself. We want to study the effect on the period of varying

• the mass of the bob
• the length of the string
• the amplitude, i.e. the maximum angle between the string and the vertical

(Note that we will use a mass on the end of a string to study the effect of mass and length variations, and we will use a rigid-rod pendulum to study the amplitude variations.) You should make sure that when varying one parameter, the others are held fixed to whatever extent possible.

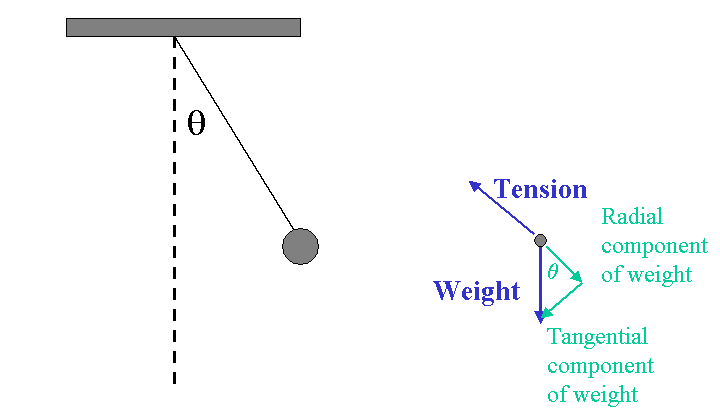
The forces acting on the bob of a pendulum are its weight and the tension of the string. It is useful to analyze the pendulum in the radial/tangential coordinate system. The tension lies completely in the radial direction and the weight must be broken into components.

The net radial force leads to radial acceleration, which is a centripetal acceleration.

where the radius of the circular motion is l, the length of the pendulum. (Recall the formula for centripetal acceleration is v²/r.) The tension and the centripetal acceleration are both directed toward the center of the circle.

The net tangential force leads to a tangential acceleration.

where the tangential acceleration is l α and α is the angular acceleration, d²θ/dt². The negative sign indicates that the net force is a restoring force, i.e., that the tangential force is in the opposite direction of the displacement from equilibrium θ.

Another approach to the pendulum is conservation of energy. At an arbitrary angle, the energy is a combination of kinetic energy and gravitational potential energy. At the highest point of the swing, the energy is entirely potential; at the lowest point of the swing, the energy is entirely kinetic (if we take the lowest point to have zero gravitational potential energy).

Substituting this expression for v_max which occurs at the equilibrium position into the expression for the tension at the equilibrium position θ=0 yields the following expression for the maximum tension: 

which will be tested toward the end of the experiment.

Experiment

• Plug a photogate into Digital Channel 1 of the Data-Studio/Pasco interface.
• Start Data Studio, click on the digital plug into the image of interface in Data Studio, and choose Photogate & Pendulum from the menu.
• Using a ringstand, clamps, a mass, some string, and so on, set up a pendulum as shown below.
  
  
  
  
  
  
• Make sure that as the bob is moving, it passes through the center of the U-shaped part of the photogate (or more importantly the little lights in the photogate).
• Initiate the pendulum's motion, record data for a few periods.
• Drag a table into Digital Channel 1 and choose Period from the menu.
  
  
• Vary the bob mass.
  
  
  • Tie bobs of different masses to the end of your string. Use the cylinders of the same size but different mass.
  • To the best of your ability, make sure that the distance between the length of the string from the crossbar to the center of mass of the bob remains fixed.
  • Make sure you release the bob from the same initial angle, you may want to use a protractor.
  • Record the masses and the periods for four different bobs.
  
  
  
  Mass Variation

  Mass         (     )	Period     (     )

  
  
  
• Vary the pendulum length.
  
  
  • Vary the length of the pendulum. To ensure a substantial range of variation, your smallest length should be less than 30 centimeters and your longest length should be close to 1 meter.
  • Keep the mass and amplitude fixed.
  • Record the lengths and periods for five different lengths.
  
  
  Length Variation

  Length         (     )	Period     (     )

  
  
  
• Vary the amplitude.
  
  
  • Replace the mass-on-a-string pendulum with a rigid-rod pendulum, which is shown below. There is a protractor on the pendulum and the angle on that protractor should be fixed at 90°.
    
    
    
    
    
  • Release the pendulum from different initial angles: 5°, 15°, 25°, 35°, 45°, and 55°. (These angles will be measured by a separate protractor and not the one that comes with the pendulum.) If 5° is too small to obtain a good measurement, then switch to 10°.
  • Record the corresponding periods.
    
    
    Amplitude Variation

    Amplitude (°)	Period     (     )
    5
    15
    25
    35
    45
    55

    
    

Maximum tension

• Close your Data Stduio file and start a new one.
• Replace the photogate with a force sensor. Force sensors are plugged into the Analog channel.
• Click on the Sampling Options button. Set the sampling frequency to 20 Hz.
• Attach the force sensor to a pole on a ringstand as shown below.
• Tare the force sensor while nothing is hanging from it. (There's a Tare button on the side of the Force sensor.)
• Tie the pendulum string to the force sensor as shown below.
  
  
  
  
  
• Attach one of the hexagonal shaped masses to serve as the pendulum bob.
• With the mass in its equilibrium position, take a force sensor reading. This reading will be the weight mg as measured by the force sensor.
• Release the mass from an angle of 20°, record a few periods of data.

Analysis.

• Plot the period versus mass. What kind of dependence if any do you see?
• Plot the period versus length. Fit it to a power law. What power do you find? Does it agree with the theoretical prediction found in your book?
• Plot the period versus amplitude. Compare your results with the theoretical prediction found in your book. Do you observe any systematic deviations from the predicted value for large angles? The derivation of this formula assumes that the angle is small, so that
  
  
  sin(θ) ≈ θ,
  
  
  
• Make a table of θ (in radians!) and sin(θ) for the amplitudes used for the above measurements.
  

  θ (in degrees)	θ (in radians)	sin(θ)	¼ sin2 (θ/2)
  5
  15
  25
  35
  45
  55

  
  According to Mathematical Methods for Physicists (G. Arfken, p. 322 in the third edition)
  
  
  
  
  
  where θ_M is the amplitude. According to this equation, does the period increase or decrease when the amplitude is increased? Does this agree with your results?
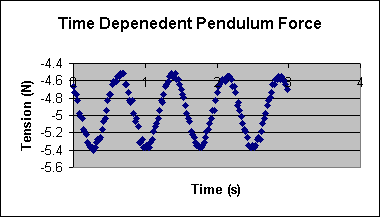
• Using the force sensor data, plot Tension vs time. Extract the tension with the maximum amplitude, which will be at the bottom of the graph. It is approximately 5.4 N in the example shown below.
  
  
  
  
  
  Compare T_max/mg to the theoretical prediction of 3 - 2 cos(θ).
  
  

  Weight from Force Sensor when still (   )	|Tmax| from Force Sensor when swinging (   )	Tmax/mg	3 - 2 cos(θ)	Percent diff.

  
  
  
• A "seconds" pendulum moves through its equilibrium position (the vertical) every second. That means that its period is 2.00 s. If you had to build a seconds pendulum, what would you use for its length, bob mass and amplitude?