Charging and discharging a capacitor: RC circuits

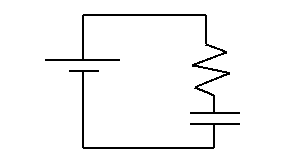
When you connect an uncharged capacitor and a resistor in series to a battery, the voltage drop is initially all across the resistor. The voltage drop across a capacitor is proportional to its charge, and it is uncharged at the beginning; whereas the voltage across the resistor is proportinal to the current and there is a current at the start. But charge starts to build up on the capacitor, so some voltage is dropped across the capacitor now. With less voltage being dropped across the resistor, the current drops off. With less current, the rate at which charge goes onto the capacitor decreases. The charge continues to build up, but the rate of that build up continues to decrease. In mathematical language, the charge as a function of time Q(t) increases but its slope decreases.

Theory says the charge obeys

where t is the time variable, C is the capacitance, V_S is the saturation voltage which in this case is equal to the voltage across the battery, and τ=RC, a time constant. The corresponding voltage across the capacitor is

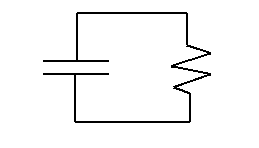
Now consider the case of a charged capacitor, a resistor and no battery. With no battery to "push" the charges around, the opposite charges on the capacitor plates would prefer to be together. They must pass through the resistor before they can reunite. With all those like charges on one plate, there is a strong incentive for charges to leave the plate. However, as charges leave the plate, this incentive decreases, thus the rate at which charges leave decreases as well. In mathematical language, this time the charge as a function of time Q(t) decreases and its slope decreases.

Theory says the charge obeys

where t is the time, Q₀ is whatever charge we happen to start with, and τ=RC is the same time constant as above. The corresponding voltage across the capacitor is

where V₀ is the initial voltage.

EXPERIMENT

Part I: Charging:

• Connect your interface to a power amplifier and set it up as a DC voltage source. (Recall DC is at the top of the drop-down list.) 
• Connect a voltage sensor (shown below) to analog channel B.
  
  
  
  
  
  
• Then in Data Studio click on the analog plug icon into the analog channel B icon and choose "voltage sensor." Drag a graph into analog channel B so we can see the data as it comes in.
• On the Signal Generator (power amplifier) set the voltage to 5.00 V.
• Make a circuit with resistor R_A and a capacitor in series (have the power amplifier "off"). Your capacitor should be discharged. Diagrammatically this circuit is represented by
  
  
  
  
• Put the leads of the voltage sensor across the capacitor. Your circuit will look something like the following
  
  
  
  
  
  The green wire represents the RC circuit (resistor and capacitor in series), while the black and red wires represent the voltage probe.
• Click Start to turn on the voltage and start recording data.
• You should see the voltage increase and "saturate" at 5.00 V. When it is fairly close to 5.00 V, stop recording, disconnect the capacitor and then turn off the signal generator. You must disconnect first so that the capacitor will have a charge left on it!
• Table the data; copy and paste the data over into Excel.
• The charging capacitor data should be described by the equation
  
  
  V(t) = V_S [1 - exp( - t / τ ) ],
  
  
  where V_S is the saturation voltage, τ is a characteristic time, and where it is assumed that t=0 is when we switched on the voltage supply.
• If you started recording before switching on the signal generator, you must adjust the time. (Ask for help if this is the case with your data.)
• Plot Voltage vs Time
• At this stage follow these instructions for fitting the data.
  
  
  Charging R_A

  VS (   )
  τ (   )

  
  
  

• With the voltage sensor across the now charged capacitor, begin recording a new set of data.
• Connect the capacitor to resistor R_A (no power supply).
• The voltage should start close to 5.00 V and decay to zero. Diagrammatically the circuit looks like the following
  
  
  
  
  
  
• Copy and paste the data (times and voltages) into Excel.
• For this case you can use the exponential option in Add trendline. Compare the τ's.
  
  
  Discharging R_A

  V0 (   )
  τ (   )

  
  
  

Part II

• Repeat the charging part of the above measurements with resistor R_B.
• Then repeat the discharging part of the above measurements with the combination of R_A and R_B in series.
• Do the plotting as above and compare τ's.
• Does the result agree with theory?
  
  
  Charging R_B

  VS (   )
  τ (   )

  
  
  
  Discharging R_A and R_B

  V0 (   )
  τ (   )
  Theory τ(   )
  Percent Error

  
  
  

Part III

• Get the measurements of the resistances R_A and R_B using the multimeter as an ohm-meter.
• Use your results to extract the capacitance. Note this is the first time we have a capacitance as opposed to a ratio of capacitances.

  RA (   )
  RB (   )

  
  
  

  	Time constant (  )	Capacitance (  )
  Charging with Resistor A
  Discharging with Resistor A
  Charging with Resistor B
  Discharging with Resistors A and B in series
  	Average (   )
  	St. dev. (   )

Use the theory of equivalent capacitance and equivalent resistance

1 / C_series = 1 / C₁ + 1 / C₂

C_parallel = C₁ + C₂

R_series = R₁ + R₂

1 / R_parallel = 1 / R₁ + 1 / R₂

to answer the following questions. Include in your report:

• What is your best estimate of the time constant if the resistors in the part-II discharging had been in parallel?
• What would happen to the time constant (increase or decrease) if we replaced the single capacitor with the combination of it and a second capacitor in series? Why?
• What would happen to the time constant (increase or decrease) if we replaced the single capacitor with the combination of it and a second capacitor in parallel? Why?