Physics 106 Laboratory: Resistors

Ohm's Law

The voltage (or potential difference) is a push that charges experience. The potential difference is measured in volts, a unit named after Alessandro Volta. This force may result in charges moving – otherwise known as a current. The current is measured in amperes or amps, a unit named after André-Marie Ampère. Actually an ampere is a fairly large current and we will see currents measured in mA (milliamps). There is a class of materials and devices made from those materials in which the current in the material is directly proportional to the voltage applied to the material; so that if one doubled the voltage, one would double the resulting current; if one tripled the voltage, one would triple the resulting current; and so on. This relationship is expressed as

V = I R

and is called Ohm’s law. Furthermore, the proportionality constant R is called the resistance; resistance is measured in ohms, a unit named after Georg Simon Ohm. Actually an ohm is a fairly small resistance and we will see resistances measured in (kilo-ohms).

Circuits, pathways that allow charges to travel around and return to their point of origin, may contain a number of resistors. There is a notion called “equivalent resistance” that says that a combination of resistors may be replaced with a single resistor that has the same effect, i.e. for any given applied voltage, the same current passes through the equivalent resistor as would pass through the combination of resistors – that is not to say that same current passes through each individual resistors, but that the same current flows into and out of the combination. Two resistors are said to be "in series" if the same current passes through each. The equivalent resistance for resistors in series is given by the formula

Req = R1 + R2

Two resistors are said to be "in parallel" if the current is split between them and them recombines after passing through them. The equivalent resistance for resistors in parallel is given by the formula

1/Req = 1/R1 + 1/R2

Our experiment will be to measure two individual resistances and then to test these formulas for equivalent resistances.

1. Insert the power Amplifier plug into Analog Channel A in the Pasco Signal Interface. If this was not the case you will have to shut down your computer, turn the interface and then the computer on. (The Power Amplifier should also be plugged in and turned on.)
2. Go to Start/All Programs/Physics/Data Studio/Data Studio.
3. Click on Create Experiment.
4. Click on the image of the interface, specifically on the image of Analog Channel A. A list of options should appear, choose Power Amplifier, and click OK.
5. A Signal Generator window should appear. Use the drop-down list to choose DC Voltage and enter 2 in the textbox under DC Voltage.
6. Connect a wire from the positive (red) signal output of the power amplifier to Resistor A.
7. Convert your multimeter to an ammeter. Insert the red lead in the mA slot and turn the dial to the mA position.
8. Insert the red needle of the multimeter into the hole adjacent to Resistor A. Insert the black needle into the negative (black) terminal of the power amplifier.
9. Click the Start button on the menu. After the current reading has settled down, record the reading in the table below. (If you get no current check that the circuit is set up properly and that the connections are good.)
10. Increase the voltage by 2 V and repeat the measurements until you reach 10 V.

If the multimeter gives no reading with the ammeter settings, then you might have to switch to one of the older ammeters as shown below. The dial on the right should be set to DC. The dial of the left should be set to either 1mA or 10mA -- the max current on that setting. Then the needle points the percentage of the max. In the picture shown, the needle points to approximately 15.7% of 10mA 0r 1.57mA.

Resistor A

For resitor A also determine the power dissipated by the resistor. Repeat the measurements for Resistor B.

Resistor B

Place Resistors A and B “in series” and repeat the measurements. (Resistors A and B are said to be in series if the current must pass through both A and B.) Note that the ammeter is also “in series.”

Resistors A and B in series

Place Resistors A and B “in parallel” and repeat the measurements. (Resistors A and B are said to in parallel if the current can pass through either A or B.)

Resistors A and B in parallel

Plot Current versus Voltage for each of the four sets of measurements. Fit the data to a straight line and extract the resistance. Compare the resistance for the series and parallel combinations to the theoretical values (i.e. use a formula). Paste the charts near the table with the corresponding data.

Kirchhoff's Rules

If two resistors are in series, then the two resistors can be added to find the equivalent resistance. If two resitors are in parallel, then the two resistors can be added reciprocally to find the equivalent resistance. However, there are arrangements of resistors which are neither in series nor in parallel. In such cases one can apply Kirchhoff's rules. One rule concerns nodes – places where wires meet. It says the currents coming into the nodes must equal the currents leaving the nodes. If this were not true, a charge (it might be positive or it might be negative) would accumulate at the node. But nodes are made from conducting materials, and charges do not accumulate inside conductors (outside perhaps, but not inside). Another rule concerns loops. It says that as one traces through a closed loop that the gains in the voltage level must equal the losses in the voltage level. An gravitation analogy in which the level is height would be that one can walk around a building changing one's height using stairs, ramps, elevators, but if one comes full circle back to one's starting point, then any increases in height are balanced by decreases in height.

• Set up the multimeter as an ohmmeter. Use the same "plugs" at the bottom of the multimeter as for a voltmeter (and different from an ammete).
• Press the 20 on the lower front.
• Insert one needle in each hole adjacent to the resistor, allow some time for the reading to settle down, and record the resistance below.
• Measure the resistances R_A, R_B, R_C, R_E, R_F and record them in the table below. (Resistances are measured when the resistor is not connected to a circuit.)
• Next, connect the resitors in a circuit like that shown below
  
  
  
  
  
  Your version may look more like this
  
  
  
  
  
  Look in the above circuit for resistors that are in series (resistors are in series if the current passing through the first is the same, no more no less, as that passing through the second). There are none! Look in the above circuit for resistors that are in parallel (resistors are in parallel if the "tops" and "bottoms" of the resistors are connected by wire and only wire). There are none. The analysis of such circuits requires Kirchhoff's rules.
• Set up the power amplifier as a DC power supply, connect it to Data Studio, etc. Set it to a volatge difference of 5 volts.
• Set up the Simpson multimeter as a voltmeter and measure the voltage across the resistors and enter them in the table below.
  
  
  Data from Kirchhoff Experiment

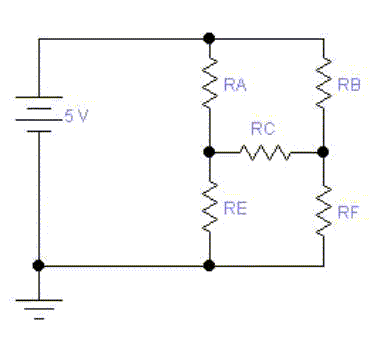
  	Resistance (    )	Voltage (    )	Current From Experiment (use Ohm's Law) (    )	Current From Theory (use Kirchhoff's rules) (    )	Percent     Error
  RA
  RB
  RC
  RE
  RF

  
  
• Obtain the experimental current from your resistances and voltages using Ohm's law I=V/R and enter them into the table above.
• Solve Kirchhoff's laws for the currents in your circuit and enter them into the table above. Include the solution in your report. (Collect the data for the second part of the experiment before performing this analysis.) One way to solve Kirchhoff's equations is by using a matrix approach, for an explanation of this approach, see this slide show on Kirchhoff. Here is a matrix equation spreadsheet like the one discussed in the slide show.