Superposition of Sound Waves

Superposition is just a fancy term for adding; in this case, we are adding waves. In Part I of this experiment we have two speakers generating waves of the same frequency but starting in different positions (and heading in opposite directions). Each wave travels from its source to a point at which we choose to detect it. In general, the waves have traveled different distances, and hence are at different parts of their cycles. If the two waves are "in sync", i.e. have their maxima at the same time, they are said to interfere constructively. The combined amplitude of oscillation at that point is greater than that of either individual wave. If the two waves are "out of sync", i.e. one has its maximum when the other has its minimum, they are said to interfere destructively. The resulting amplitude of oscillation is less than that of either individual wave.

In Part II, there is only one speaker at the end of a tube, the second wave in question is a reflection of the first. We will look for incidents of resonance, situations in which the wavelength and length of the system "match up" leading to constructive interference and hence increased intensity. (Do not read "matching up" as "being equal.") "Matching up" means different things depending on whether the tube has open ends, closed ends or one of each.

In Part III, we have again two speakers, but this time with slightly different frequencies. In this situation, the two waves may be in sync at one time and out of sync another time even if the position of measurement is not changed. We will look for variations in the intensity as a function of time (beats) rather than space.

Part I.

• Connect the power amplifier to the interface analog channel A (as done last week).
• Connect the amplifier to two speakers. (The same terminal of the amplifier should be connected to the identical terminal on the speaker, e.g. connect the lower power amplifier terminal to the terminal on the outer edge of both speakers.)
  
  
  
• Click on the image of the analog plug in Data Studio, choose Power Amplifier.
• Choose an AC sine waveform of 1010 Hz. Calculate the wavelength of the sounds waves at this frequency.
  
  
  Freq. = 1010 Hz

  Wavelength (     )

  
  
• Connect a microphone to Analog Channel B.
• Click the image of the analog plug in Data Studio and choose Sound Sensor.
• Click on Sampling Rate on the right-hand-side of Data Studio and change the sampling frequency to 100 Hz.
• Under that use the drop-down list to change the sensitivity to Medium.
• Place two speakers facing each other 1.00 meter apart.
  
  
  
  
  
• Place a meter stick between them (with the 50-cm mark in the middle of the speakers).
• Drag a graph into channel B.
• Place the microphone (be sure it's on) at the 50-cm mark.
• Turn on the signal generator and briefly record some data.
• You can click on the vertical scale of the graph if your graph is not using the full height of the graph. 
• Next beginning again at 50-cm, record data moving the microphone 2 cm every 5 seconds (stop watches are available). The data should then correspond to the following table. (You are recording sound, so be as quiet as possible.)
  
  

  Time (s)	Position (cm)	Path difference (cm)
  0-5	50	0
  5-10	48	4
  10-15	46	8
  15-20	44	12
  20-25	42	16
  ...	...	...

  
  Take data for at least one full minute. Moving the position 2 cm changes the path difference 4 cm. Why?
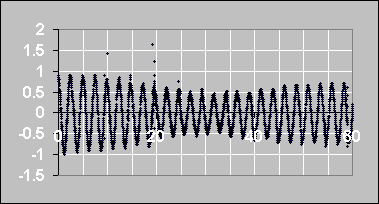
• Table the data, click on the clock, copy and paste the data over to Excel and make a plot. It should look like the following
  
  
  
  
  
• You can see the amplitude differs for the various 5-second intervals. Because of procedure used, you can identify a time interval with a positon. Note the positions of the minima or maxima in intensities that you observe. You are NOT looking at individual maxima and minima in the curve above; you are looking at amplitudes for different five second periods.
• What are the measured and theoretical positions of maxima and minima?
  
  

  	Measured	Theoretical
  First maximum
  First minimum
  Second maximum

  
  
  
• Switch the leads (where the wires plug in) on one of your speakers.
• Repeat the process above beginning midway between speakers. What happens? Why?
• What are the measured and theoretical positions of maxima and minima?
  
  
  Switched Leads

  	Measured	Theoretical
  First maximum
  First minimum
  Second minimum

  
  
  

Part II.

• Connect your power amplifier to the small speaker at the end of the long tube. (You can also use the portable function generators which you may be able to take into another room where it is quieter.)
  
  
  
  
  
• Input a 1700 Hz signal. What is the wavelength corresponding to this frequency?
  
  
  Freq. = 1700 Hz

  Wavelength (     )

  
  
• Move the plunger the entire length of the tube. You should hear a modulation in the intensity. (This may require some cooperation among neighboring groups.)
• Note the plunger positions (to the nearest tenth of a centimeter, if possible) at which these intensity maxima occur. Be careful to distinguish positions at which the intensity is a maximum from positions at which the intensity changes most rapidly.
  
  
  Freq. = 1700 Hz

  Positions of Maximum Intensity (     )

  
  
• Based on the plunger positions where you find resonances, determine whether the tube has open-open or open-closed boundary conditions. Explain your reasoning.
• Repeat the measurements and analysis with an 850 Hz signal.
  
  
  Freq. = 850 Hz

  Wavelength (     )

  
  
  
  Freq. = 850 Hz

  Positions of Maximum Intensity (     )

  
  

Part III.

• You will need two signal generators for this part. Team up with another group if need be.
• You will have to reset the Sample Rate, which may require closing and reopening Data Studio. Put the Sample rate of the Sound Sensor at 2000 Hz.
• Attach one speaker to each signal generator.
• Set one at a frequency of 400 Hz, the other at 402 Hz.
• Place the two speakers near one another and see if you can hear the beats (undulations in intensity).
• Next place a microphone near the speakers and record the sound from the two speakers.
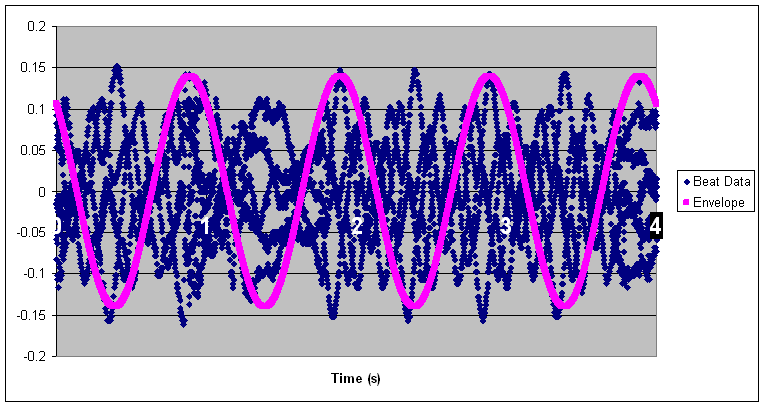
• Take your data (a couple undulations worth) over to Excel and try to fit the "envelope function." It may help to review the first lab. Your graph should look something like the following
  
  
  
  
  If it does not, see the instructor.
• Put somewhere in your report the equation of your fit function.
• From the graph extract your "beat frequency". How does it compare to the frequency of your envelope function?