PYL 106: January 18

Oscillatory Motion

When a mass is hung vertically from a spring, the spring stretches. There is a point at which the spring force and the weight are equal in magnitude but opposite in direction. This point is called the equilibrium position. If the mass is in any other position, there is a net force called the restoring force directed toward the equilibrium position. The restoring force results in the mass eventually returning to the equilibrium position. The mass, however, picks up some momentum and continues past the equilibrium position causing the same situation as before but on the opposite side of the equilibrium position. The outcome is a repeated motion in which the mass passes through the equilibrium position, turns around, heads back toward the equilibrium position, passes through it, and so on. Such behavior is called oscillatory motion.

The position of a mass oscillating on a spring can be described by the following equation

y(t) = y_eq + A cos ( 2 p t / T + f ).

It is assumed that the argument (the stuff in the parentheses, a.k.a. "the phase") is in radians and NOT degrees. Note that there are four parameters

y_eq: the equilibrium position, determines the midpoint of the motion
A: the amplitude, determines the size the the oscillations, i.e. the maximum displacement from the equilibrium position
T: the period, determines how much time goes by before the motion begins to repeat itself
f: the phase constant, determines the part of the cycle at the beginning (t=0)

Experiment

Plug a motion sensor into the signal interface (which should have been turned on before the computer), the yellow plug should go into Digital Channel 1, the other into Digital Channel 2.
In Science Workshop, drag the digital channel icon into Digital Channel 1 and choose Motion sensor. Set the trigger rate to 60 Hz. For our sensors to work properly the mass and the sensor should be at least 0.5 meters apart.
Place a mass on a spring hanging from a tall ringstand with a motion sensor positioned beneath as shown below.
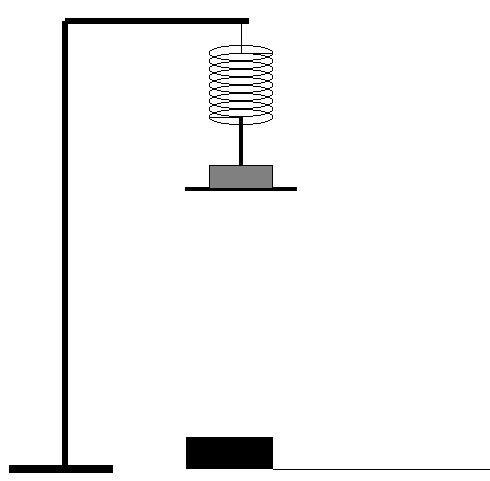
Record the mass, don't forget to include the mass of the hanger.
Set the mass into oscillatory motion (stretch the spring a few centimeters and release) and begin recording data. You only need to record a couple cycles. Try to ensure that the motion is vertical.
Within Science Workshop, make a table of the position data. Click on the clock to get the times as well.
Copy the column generated and paste it into an Excel spreadsheet.
Repeat this procedure with several different masses (at least three others, changing the mass by at least 50 g).

Analysis

For each of the masses, plot position versus time [an XY (Scatter) Chart in Excel]. On the same graph, plot a mathematical function that resembles as much as possible your data.
(Click here for some help with this.)
You should be able to identify in your function the equilibrium position, the amplitude, period and phase constant associated with this oscillatory motion. Include in your report a table of the masses and this information.
Plot weight (mass times g) versus y_eq and fit it to a straight line. Extract from the fit the force constant of the spring k.
Make a graph of the period T versus mass. Use the Add Trendline feature to fit your curve to a power law. The Display equation on chart option will tell you what power law fits best. (Ask if you don't know what I mean.)
Compare your periods to the theoretical values
T = 2 p ( m / k )^1/2.
Suggest a source of systematic error in this comparison.