

 PYL
105: Lab 10
PYL
105: Lab 10



Collision Carts and Conservation of Momentum
You can find the material related to
this lab in Serway, Chapter 8.
The momentum of an object is the product of its mass and its
velocity.
p = m v
The bold letters are used above to convey that momentum,
represented by the p, is a vector.
In addition to the momentum of a single object, one can consider
the momentum of a "system" -- a combination of related objects.
P = p1 + p2 + ... =
m1 v1 +
m2 v2 + ...
The quantity P is useful because it is conserved (does not change
with time) under certain circumstances.
The circumstances are when there is no net external force on the
system.
Fnet,ext = 0
By "external" we mean forces exerted by bodies that are not
part of the system on bodies that are part of the system.
The claim is that internal forces, forces exerted by one body
in the system on another, do not affect P, the momentum
the system.
- Find the mass of two collision cars and two metal blocks
and enter them in the table provided below.
Your collision cars should have ends with Velcro patches.
- Set up a motion sensor (with a frequency of 20 Hertz) at
the end of a track.
- Place Cart 1 near the end of the track with the motion
sensor and Cart 2 in the middle of the track, as shown below.
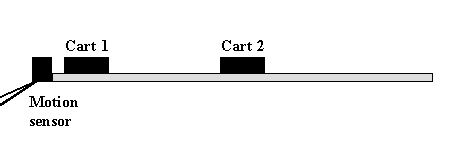
- The Velcro ends should be facing each other, so that the
carts will stick together when they collide.
- Start recording and give Cart 1 a quick push.
- Our analysis will be based on the assumption that the carts
stick together. Throw out the run if this was not the case.
- Make a plot of the velocity versus time
data eliminating any bad data at the beginning and end of
recording. It should look something like the graph shown below.
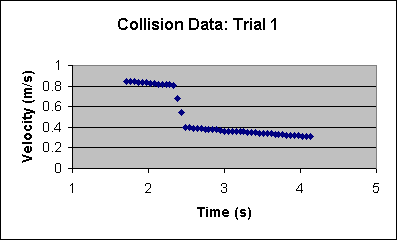
- The sharp fall off in velocity (around t=2.4 s in the
graph above) occurs when the carts collide and stick together.
Find the velocity of Cart 1 just before the collision and
the velocity of the Cart 1/Cart 2 combination just after the
collision. Record these in the table provided below.
- Calculate the momentum of Cart 1 just before the collision
and just after the collision. Also calculate the momentum of
Cart 2 after the collision. Enter them in the table provided
below.
- Calculate the momentum of the system just before and
just after the collision as well as the percent difference and enter them in
the table provided below.
Repeat the measurements and calculations for the following cases:
- Trial 2: add one block to Cart 1.
- Trial 3: add a second block to Cart 1.
- Trial 4: remove the blocks from Cart 1; add one block to
Cart 2.
- Trial 5: add a second block to Cart 2.
Don't forget to include the mass of the block(s) in your
calculation of momentum.
DATA AND CALCULATIONS
Masses
| Item | Cart 1 |
Cart 2 |
Block 1 | Block 2 |
| Mass (kg) | | |
| |
Velocities
| Trial | Velocity before
Cart 1 (m/s) |
Velocity after
Carts 1 & 2 (m/s) |
| 1 | | |
| 2 | | |
| 3 | | |
| 4 | | |
| 5 | | |
Individual momenta
| Trial | Momentum before
Cart 1 (kg m/s) |
Momentum after
Cart 1 (kg m/s) |
Momentum after
Cart 2 (kg m/s) |
| 1 | | | |
| 2 | | | |
| 3 | | | |
| 4 | | | |
| 5 | | | |
Momentum of the system
| Trial | Momentum before
System (kg m/s) |
Momentum after
System (kg m/s) |
Percent difference |
| 1 | | | |
| 2 | | | |
| 3 | | | |
| 4 | | | |
| 5 | | | |
The change in mometum is equal
to the "impulse", the force integrated over time.
I = pfinal -
pinitial
We can find the average force exerted on Cart 1 by Cart 2 during
the collision by taking the change in momentum of Cart 1 and
dividing it by the duration of the collision.
Fave = I /
D t
We can estimate the duration by examing the velocity versus
time graph made earlier.
Take the last point of the upper line and the first point of
the lower line and finding the difference in the two times.
Impulse and average force
| Trial | Impulse
Cart 1 (kg m/s) |
Duration
(s) |
Force of Cart 2
on Cart 1 (N) |
| 1 | | | |
| 2 | | | |
| 3 | | | |
| 4 | | | |
| 5 | | | |
There are external forces acting on the two-cart system. What
are they?



 PYL
105: Lab 10
PYL
105: Lab 10





