PYL 105: Lab 2

One dimensional kinematics

With this lab we begin our experimental study of motion. We will be studying how the position changes as a function of time, thus we will be measuring positions and times. A motion sensor will take both sets of measurements for us.

One of the first steps in studying motion is to establish a coordinate system, which associates a number with a particular point in space. The point associated with the number zero is known as the origin. In this experiment the origin is determined by the motion sensor; positions will be measured relative to it. The motion sensor also has a built in clock. According to the motion sensor, time is zero when we start recording data.

We will collect data on the position of a cart as a function of time. The cart's velocity is the rate at which its position is changing. Graphically the (instantaneous) velocity at a particular time is the slope of the Position versus Time curve at that time.

We will see that the velocity (the slope of the x-t curve) changes in the course of the experiment. We can then study the rate of change of the velocity, which is known as acceleration. Graphically the (instantaneous) acceleration is the slope of the Velocity versus Time curve. If the acceleration changes, we can study its rate of change, and so on.

Part I: The push

• Turn on the Pasco Signal Interface. (Recall it must be turned on before the computer.)
• Obtain a track, cart and motion sensor and set them up as shown below.

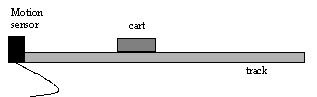
• Insert the motion sensor's's yellow plug in Digital Channel 1 and the black plug in Digital Channel 2.
• Start Science Workshop (Start/Programs/Physics/ScienceWorkshop/Science Workshop).
• Drag the Digital Plug icon into the Digital Channel 1 icon.
• Choose Motion Sensor from the menu and click OK.
• Place the cart about 60 cm from the motion sensor. (The motion sensor is inaccurate for measuring distances smaller than 50 cm.)
• Click the REC (record) button, give the cart a quick push away from the sensor.
• Click the STOP before the cart has reached the end of the track or stopped.
• Drag the Table icon into the Digital Channel 1 icon. Choose Position from the menu. A table of positions should appear.
• On the table, click on the button resembling a clock (upper left) to obtain the corresponding times. (This is the position as a function of time data mentioned above.)
• With the table showing choose Edit/Copy from the menu.
• Open an Excel workbook and paste the data into it.
• Make an XY Scatter graph of Position versus Time.
• Repeat the last 5 steps but choose Velocity instead of Position.

Using your graphs, identify the various intervals

Interval Type	Start time	End Time
The time between pressing REC and the beginning of the push
The duration of the push
The cart traveling down the track after the push

• Repeat the measurements above with one difference: have someone stop the cart before you stop recording data.
• Make the Position versus Time and Velocity versus Time graphs.

Identify the various intervals

Interval Type	Start time	End Time
The time between pressing REC and the beginning of the push
The duration of the push
The cart traveling down the track after the push
The cart being stopped

It is important when solving problems to identify the regions that have different "physics" (in this case different forces acting on the object). It should be clear in the graphs that the cart behaves differently when it is in contact with your hand. Since the behaviors (shapes of the curve) are different, different equations apply. Hence, when we compare the data to theory, we have choose a region (interval). Let us select out the data corresponding to the cart traveling down the track (no hands). Why did we choose this region? Fit the velocity versus time data in this region to a straight line. If the fit is good, then we can conclude that the acceleration is constant. Is your fit good? If so, what is the acceleration?

Part II: The tilt

An important feature of experimental work is reproducibility. The problem with the measurements in the first part of this lab is that it is difficult to push the cart with the same force and duration each time we do the experiment. For a reproducible cause of motion we can tilt the track at an angle, re-enacting a famous experiment done by Galileo. If the tilt of the track is the only force (i.e. no friction, no air resistance) then theory says that the acceleration does not depend on the mass of the object.

• Using a balance, determine the mass of an empty cart.
• Prop the track up on a small wooden block so that it is slightly inclined and place a motion sensor at the track's end as shown below.

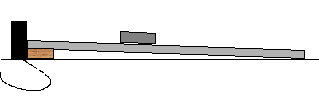
• Place the cart about 60 cm from the motion sensor.
• Click REC and release the cart (do not push it). Click STOP before the cart reaches the end of the track.
• Plot Velocity versus Time, fit it to a straight line, and extract the acceleration.
• Determine the mass of one of the black rectangular blocks that fit into the cart.
• Place the mass in the cart, measure and graph the velocity-versus-time data.
• Add the second block and repeat.

Cart Mass (kg) (inc. block)

Experimental Acceleration (m/s^2) (from graph)

Theoretical Acceleration (m/s^2) (from eq.)

In the absence of friction and air resistance, theory says that the acceleration is given by

a = g sin (q)

where q is the angle between the track and the lab table (horizontal) and g is 9.8 m/s² , the acceleration due to gravity. Find q. Caution: the angle is small and attempting to measure it with a protractor will probably result in a significant amount of error. Use trigonometry. How do your results compare with the above prediction?

In part I, you should have observed deceleration, and in this part, you should have observed acceleration. Imagine selecting an angle such that the two effects exactly balanced, what would the velocity-versus-time graph look like in this instance?

Part III: The pulley

In the case of the tilt, the cart (in particular its mass) plays a dual role. It is the thing being accelerated, and it is the cause of the acceleration (the gravitational attraction between the mass and that of the earth). Now we will consider a situtaion in which the cause of the object's acceleration is not its weight.

• Set the track on two of the larger blocks so that it is level.
• At one end use a universal clamp to secure a pulley at track level.

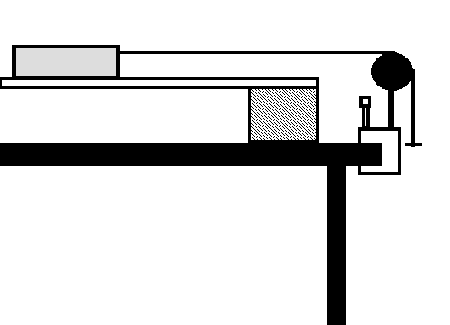
• Place the motion sensor at the other end.
• Tie one end of a string to an empty cart, pass it over a pulley and tie the other end to a hanger.
• Place the cart so that the string is taut and the hanger hangs just below the pulley.
• Begin recording data and release the cart.
• Plot velocity versus time and extract the acceleration. Please note that if the hanger hits the floor, the "physics" changes. Before you let the cart go, measure the distance from the floor to the bottom of the hanger and make sure that you stop the cart before it goes that far. Then you can use the kind of observations made in Part I to keep the data up to but not including the time you stopped the cart.
• Add a block to the cart and repeat the measurements.
• Add the second block and repeat.

Cart Mass (kg) (inc. blocl)

Experimental Acceleration (m/s^2) (from graph)

Theoretical Acceleration (m/s^2) (from eq.)

In the absence of friction and air resistance, theory predicts that

How do your results compare to theory?

Distinguish between the mass-dependence of the accelerations you find for the tilt and for the pulley set-ups.

Part IV: Sketching

Suppose a mass were sliding along a track like the one shown below.

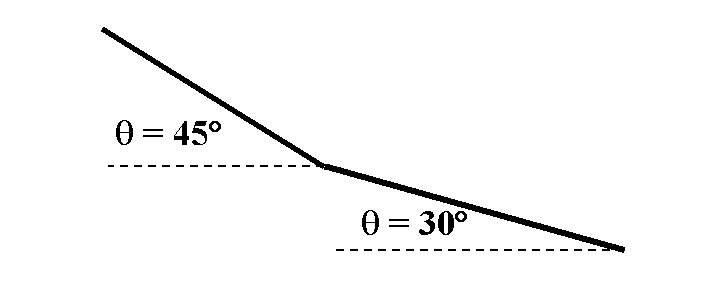
Sketch a graph of what the velocity-versus-time graph would look like.