Forces and Vectors

Forces have a both a magnitude and a direction. The magnitude tells one the size of the push or pull supplied by the force, while the direction tells which way the object is being pushed or pulled. Forces are thus represented mathematically by vectors. A quantity must have certain properties in order for it to be considered a vector. For instance, there are rules expressing vectors in terms of components and rules for adding vectors.

Expressing a vector in terms of its components is also known as "resolving" it. Let us consider resolving a force F into components. Find the angle between the x axis and F as shown below. There are two conventions for measuring angles:

1. To measure the angle starting from the positive x axis, proceeding in a counter-clockwise direction and ending on the vector of interest. This approach results in angles between 0 and 360 degrees.
2. To measure the angle between the x axis (positive or negative, whichever is closer) and the vector of interest. This approach yields angles between 0 and 90 degrees, and one must further keep track of which quadrant the vector lies in.

We'll adopt the second method in the following discussion. Another thing to keep in mind when dealing with angles is to keep track of whether one is working with degrees or radians.

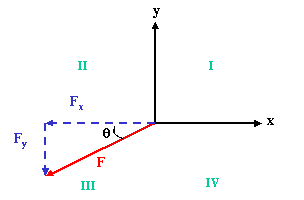
We can think of F and its x and y components (F_x and F_y) as the sides of a right triangle, with F as the hypoteneuse and the components as the legs. Using the trigonometric relation that

we can determine that with the angle as drawn above, F_x, the x component of F is, up to a sign, given by

where |F| is the magnitude of F. Similarly, up to a sign the y component of F₃ is given by

the magnitude of F times sin theta. The signs can be determined by what quadrant one is in

Part I. Calibrating the Force Sensor.

• Attach a force sensor to a ringstand as shown below.
  

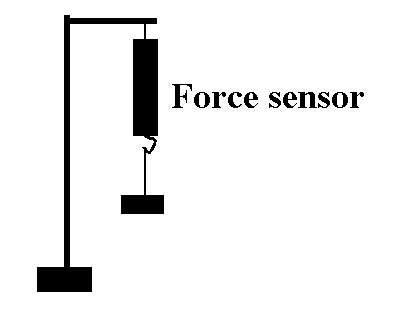
• As usual the Signal Interface should have been turned on before the computer. Plug the Force Sensor into Analog Channel A. Bring up Science Workshop and drag the analog plug icon into the Analog Channel A icon, and choose Force Sensor from the menu.
• BEFORE hanging a hanger from the Force Sensor, press the TARE button on the side of it. This step is supposed to establish the "zero" of the Force Sensor.
• Hang the hanger from the force sensor. Add a mass of 100 g.
• Press REC and take force data for a few seconds.
• Table the data and press the SIGMA button to obtain the mean force. We are only interested in getting the magnitude of the force (which is necessarily positive) from the source, so you don't have to worry about the negative sign the force sensor gives.
• Repeat the measurements with 200 g and 300g on the hanger.

  Mass (kg)	Force (N) (Measured)	Force (N) (Theory, mg)
  0.150
  0.250
  0.350

Do you observe any errors in your force sensor readings? If so, are they systematic or random? Explain.

Part II. Resolving the force vector into components.

• Tie three strings to washer. Two of the strings should be of a length such that if the washer is in the center of the force table, the strings can pass over a pulley at the edge of the table and hang several centimeters below table level.
  
  
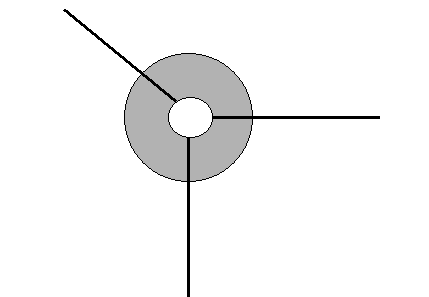
• Attach the two longer strings to hangers, and we want the hangers to hang several centimeters below the pulleys and several centimeters above the lab table as well.
• The length of the third string should be slightly longer than the radius of the force table. We will be attaching the third string to the Force Sensor.
• Put one pulley at 360 and the second at 90. Place the longer strings over the pulleys and suspend hangers from them. Add unequal masses (at least 100 g) to the hangers and determine the weight of each (multiply by g=9.8 m/s², don't forget the mass of the hanger).
  

• Attach the hook of the Force Sensor to a loop at the end of your shorter string. Hold the Force Sensor so that the strings attached to the washer are horizontal (not vertical!) and so that the washer is over the center of the force table. Hold it there as steadily as possible while one partner clicks on Record in Science Workshop -- you only need a few seconds. Also note the angle of the string attached to the Force Sensor (the angles are marked on the Force Table). Some groups attaching the Force Sensor to a ringstand.
• Record the mean magnitude of the force.
• We will first want a coordinate system; we will take the x direction to point in the radial direction from the center of the table toward the 360 degree mark and the y direction to point in the radial direction from the center of the table to the 90 degree.
  
  Let us draw the three forces in this coordinate system.
  
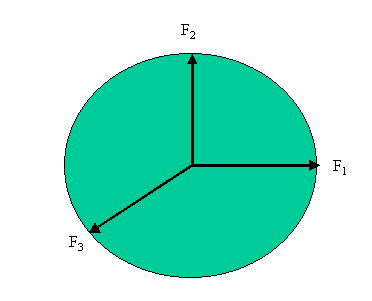
  (Sometimes when picturing vectors the lengths of the lines are meant to be proportional to the magnitudes of the vectors. This is not true in this picture.) The way we have set it up and the way we chose the coordinate system F₁ has only a positive x component and F₂ has only a positive y component.
• The way vectors add is that one adds their components. So the x component of the net force (F₁+F₂ + F₃) will in this case be
  F₁ + F_3x

  and the corresponding y component will be

  F₂ + F_3y

  For a vector to be zero, all of its components must be zero. Thus the two expressions above should yield zero. Verify this.

  	Magnitude	Angle	Quadrant	Fx	Fy
  Force 1
  Force 2
  Force 3
  Sum

• Change one of the masses (make a change of at least 50 grams) and repeat the measurement and calculations.

  	Magnitude	Angle	Quadrant	Fx	Fy
  Force 1
  Force 2
  Force 3
  Sum

Are the sums of the components acceptably close to zero? (Take into account any Force Sensor errors you observed in part I.)

Part III. Adding vectors.

• Add a fourth string to your setup and place it at angle between 30 and 60 degrees and attach it to a hanger. Our goal now is to replace two of the tensions (the force exerted by a string is referred to as tension) by a single tension that serves the same purpose in balancing the washer. First measure F₃ (the Force Sensor force) as in Part II (obtain the magnitude and the direction).
• Now add the vecrors representing F₁ and F₄ by first resolving F₄ into x and y components and adding the components.
• Adding the components of F₁ and F₄, you now have the components of the sum, which we will call G.
• We now need to find the magnitude and direction of G. If G_x and G_y are the components, then the magnitude of G is given by
  |G| = (G_x² + G_y²)^1/2

  (Pythagorean theorem) and the direction (angle) by

  q = Arctan (G_y/G_x).

• Make the replacement you just determined. i.e. let the string giving F₂ alone, but remove the fourth string and change weight hanging on string 1 to correspond to the magnitude of G, and change its angle to the direction of G.
• Then remeasure F₃. It should be essentially unchanged. In you report you should give all the vectors before, show you work to determine the "resultant" (the sum) and show your measurements (all the vectors) after.
    

  	Magnitude	Angle	Quadrant	Fx	Fy
  Force 1
  Force 4
  Force G
  Force 3 (before)
  Force 3 (after)

• Repeat the set up with four strings again, but this time change all of the angles. Strings 1 and 2 should no longer be at 360 and 90. Add vectors 1 and 4 as before. (This time you will have to resolve both vectors into components before adding.)
• Then repeat the above measurements and calculations.   

  	Magnitude	Angle	Quadrant	Fx	Fy
  Force 1
  Force 4
  Force G
  Force 3 (before)
  Force 3 (after)

Did Force 3 change substantially when you replaced Forces 1 and 4 with Force G? Are any differences acceptable? Explain.

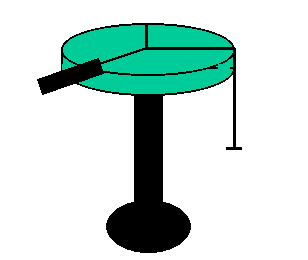
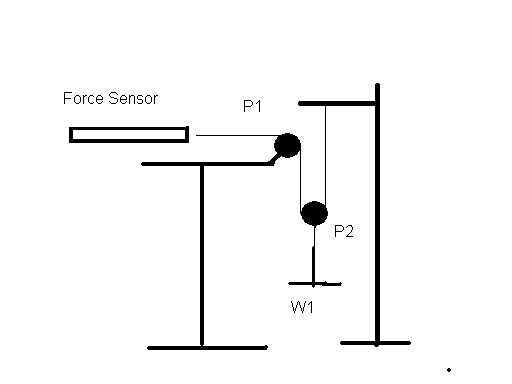
Part IV Pulley Effect

Arrange your apparatus based on the figure below.  When W1 (pan and added mass) has a mass of 100g what is the sensor's reading?  Repeat with 150g, 200g and 250g.  What is the sensor holding up?  With the 250g attached slowly pull the force sensor 4cm.  By how much does W1 move?