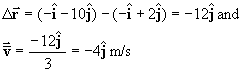PHY 105 Test 2 May 23, 2002 30 minutes
La Salle University
Dr. R. A. DiDio
1. [15 pts] A helicopter is flying
horizontally at 60.0 m/s when a front wheel falls off. The altitude of the helicopter is 300 m when
this occurs.
a)
How much time is required for the tire to hit the earth?
|
Solution: This is a projectile problem with an
initial height above the ground (300 m), and only a horizontal velocity (60
m/s). Therefore, tAir can
be calculated from: |
b)
How far does it travel horizontally while falling?
|
Solution: Given the air time and the initial
horizontal velocity, the range is determined by |
c)
Find the horizontal and vertical components of velocity when
it hits the ground.
|
Solution: The x-component of velocity is still 60
m/s. The y-component of velocity is
determined by |
2. [10 pts] A subway train starts from
rest and accelerates at a rate of 1.60 m/s2 for 14.0 s. It runs at constant speed for 70.0 s and
slows down at a rate of 3.50 m/s2 until it stops at the next
station. What is the total distance covered?
|
Solution: There are three legs on this trip – Leg I – Constant acceleration
of 1.6m/s2 for 14 s: Leg 2 – Constant velocity
for 70 seconds. The velocity is the
velocity after the initial 14 second acceleration:
Leg 3 – Negative acceleration
of –3.5 m/s2 from 22.4 m/s to 0 m/s. Since you know beginning and ending velocities, find the
distance traveled using
Total Distance
Traveled = 156.8 + 1568 + 71.68 m = 1.80 x 103 m |
3. [10 pts] A particle is at position (-1
m, 2 m) in the x-y plane, moving with velocity ![]() . It experiences constant acceleration of
. It experiences constant acceleration of ![]() for 3 seconds
for 3 seconds
a)
Where is the particle after 3 seconds? (Express your answer
as a position vector)
|
Solution: Use the vector form of the motion with
constant acceleration: (Note – all position, velocity, and acceleration are
in appropriate SI units)
In this problem
At t = 3 s,
|
b)
What is the average velocity of the particle in the first 3
seconds?
|
Solution: Use the vector definition of average
velocity
Using the initial
positon and the position from (a) as r1 and r2,
respectively,
|