Capacitors

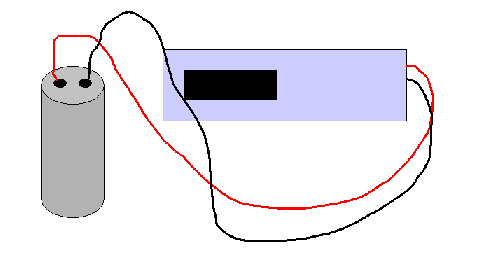
Imagine a situation in which you have two conductors separated by some non-conducting material, as shown below.

Imagine that you can push positive charges through conductor A (on the left) until they reach the edge, where they are trapped. Those charges affect conductor B (on the right), which was neutral but composed of positive and negative charges. The positive charges in A attract the negative charges and repel the positive charges in B. Those positive charges are pushed away to some distant place. The end result is these two nearby conductors, one with a positive charge, the other with a negative charge.

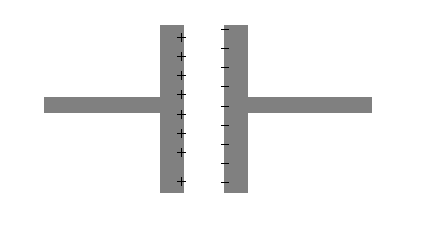
This is called a capacitor.

There is no electric field due to these charges inside the conductor (because of the above considerations). But there is an electric field between the conductors pointing from the positive charges to the negative charges, as shown below.

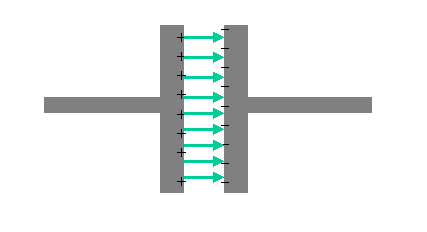
Recall the the electric field is related to the slope of (the change in) the electric potential. Therefore the electric potential must be changing, and we can talk about the potential difference (denoted V, a.k.a. the voltage).

The potential difference between the conductors is proportional to the charge Q on a plate. We are lead to the following relationship

The proportionality constant between V and Q is 1/C, where C is called the capacitance.

In this lab we will measure the equivalent capacitance of combinations of capacitors.

Part I. (Capacitors in parallel)

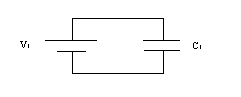
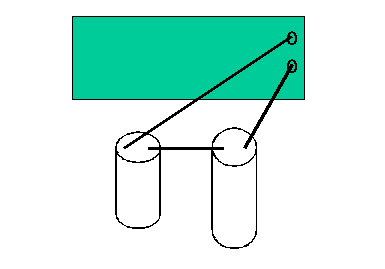
Geometry (size and shape) is a factor in determining capacitance. We will be working with three different sized capacitors, and hence three different capacitances: C₁, C₂ and C₃. Let us call the largest one C₁, the middle one C₂ and the smallest C₃. We would have to know the voltage V and the charge Q to determine C. We can use a voltmeter to measure V, but we cannot directly measure Q. Therefore, we will instead determine the ratios C₂/C₁ and C₃/C₁ from our measurements.

• Insert the power Amplifier plug into Analog Channel A in the Pasco Signal Interface. (The Power Amplifier should also be plugged in and turned on.)
• Click on the Science Workshop icon on the desktop.
• Drag the Analog Channel icon into the Channel A icon and choose Power Amplifier.
• A Signal Generator window should appear. Choose DC and click on the number under DC Voltage and enter 5.
• Connect C₁ to the Power supply as shown
  
  This is drawn diagrammatically as:
  
  
• Apply a voltage of 5 volts across C₁ and disconnect it (while the voltage source, the signal generator is still on). You can use a DC voltmeter to check that you have charged up the capacitor. (It should read close to 5 volts.) To use a multimeter set up as a DC voltmeter, make sure the V button is pressed and that the DC button is pressed (the buttons may have wavy lines for AC and straight lines for DC). The multimeter may have three holes with two leads (wires) coming out. If so make sure the upper lead is plugged into the hole that indicates V (not A). Put one needle into each side of the capacitor as shown below.
  
  If the voltage reading is negative, switch the leads.
• Next connect C₁ to C₂ as shown. You should make sure C₂ has no charge to start with. How?
  
  When capacitors are in such an arrangement, they are said to be in parallel. Things in parallel should have the same voltage.
• Disconnect them and measure the voltages across each, V₁' and V₂' (they should be very close).

  	Voltages (V) Trial 1	Voltages (V) Trial 2
  V1
  V1'
  V2'

• We have three equations:
  1. V₁ = Q₁/C₁
  2. V₁' = (Q₁-q)/C₁
  3. V₂' = q/C₂.

  where Q₁ is the charge on C₁ before C₂ is added and q is the charge that goes over to C₂.

• We need to eliminate Q₁ and q. Solve the first equation for Q₁ and the third equation for q.
• Substitute both of these results into the middle equation. The resulting equation has V's which we know and the ratio C₂/C₁ which we want.
• Repeat the above measurements making sure you obtain consistent results. The most common mistake is to forget to discharge the capacitors before starting. If your results are not consistent, repeat again.
• Repeat the measurements and calculations to determine C₃/C₁.

Another way to determine the ratio C₂/C₁ is to put C₁ and C₂ in series, as shown below.

• Set the signal generator to 5 Volts DC.
• First make sure to discharge your capacitors before starting.
• After charging up the capacitors in series, disconnect them from the circuit and each other and measure the voltages across each. (The two voltages should add up to close to 5 V.)

  	Voltages (V) Trial 1	Voltages (V) Trial 2
  V1
  V2

• In the series arrangement, the charge on the second capacitor comes from the first and thus they are equal. Hence we have the following set of equations
  1. V₁ = Q₁/C₁
  2. V₂ = Q₂/C₂
  3. Q₁ = Q₂.

• We can again solve for the ratio.
• Compare it to your result from Part 1.
• Repeat the measurements and calculations to obtain C₃/C₁ as well.

  	Voltages (V) Trial 1	Voltages (V) Trial 2
  V1
  V3

  	Trial 1	Trial 2
  C2/C1
  C3/C1

Put C₂ and C₃ in parallel. (Discharge first.) Then repeat the measurements in Part II but with the parallel combination in place of an individual capacitor.

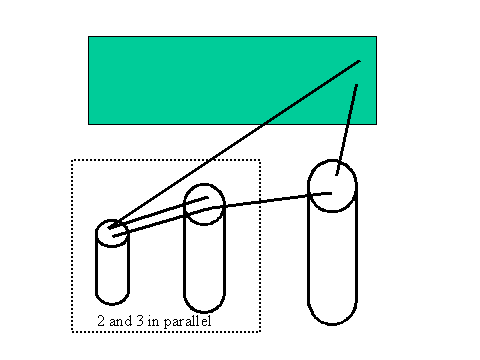
Never separate C₂ and C₃, always treat them as a combination.

so that in terms of ratios we have

Next, discharge your capacitors and then put C2 and C3 in series, as shown below.

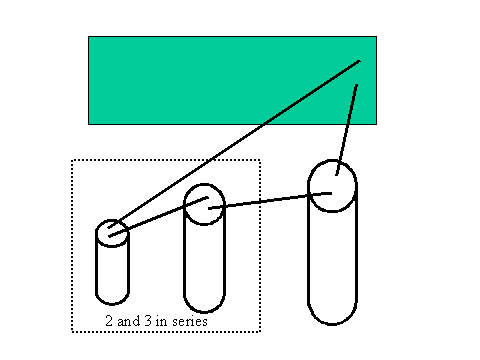
Find the ratio of the equivalent capacitance C_eq' = C_2S3 to C₁ and compare it to the theoretical prediction.

so that

To calculate the theoretical results use the average of your (trusted) results for C₂/C₁ and C₃/C₁ from Parts 1 and 2.