

 PYL 106: Standing Waves
on a string
PYL 106: Standing Waves
on a string 



Standing waves on a string
When you throw a rock into a pool,
the water is disturbed. The water is shifted away from its equilibrium position,
the flat surface. This disturbance then moves in what we call a "traveling
wave." If a wave happens upon an abrupt edge (like the pool wall), it will be
reflected back. When there are two waves traveling in opposite directions, a
possible outcome is a "standing wave."
In such a situation, the disturbance does not appear to move but rather just
to oscillate in place. In fact, each point is undergoing periodic motion, all
with the same period. While the periods are all same, the amplitude varies from
point to point. But of course, two points that are very close must have nearly
the same amplitude. There are special points, called nodes, which have no
amplitude at all. Below is a picture of a standing wave where the different
lines represent the wave at different times.
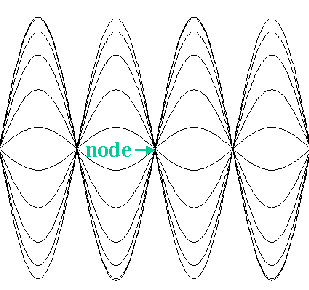
In addition to the notion of period T (the time required for
the motion to repeat itself), with harmonic waves one has the concept of
wavelength l (the distance between two
points that are undergoing identical motion). One has to be careful here. Our
eyes tend tend to average what is happening over time. Two points that seem to
be udergoing identical motion may in fact be undergoing opposite motion but when
"time-averaged" appear to us to be identical. The speed of a wave is given
by
v = l / T
(When we talk about speed in a standing wave, we mean the speed of the two
individual waves that make up the standing wave.) We can measure l and T and determine this speed. If the wave in question is
on a string, theory provides us with another expression for speed
v = (F / m )1/2
where F is the tension in the string and m is the
linear mass density (mass/length). One may see this equation written with a T
for tension in place of F. Be careful not to confuse tension T with period T.
Experiment
- Plug in the power amplifier and connect it to the signal interface (use
analog channel A). Turn it on.
- Connect the output of the amplifier to the speaker (two wires needed: one
from the red terminal on the power amplifier to the speaker, the second from
the speaker back to the black terminal of the power amplifier). One needs a
complete circuit.
- Start up Science Workshop (Start/Programs/Physics/Science Workshop/Science
Workshop) and drag the analog plug into analog channel A and choose "power
amplifier." (Was the interface on before the computer?)
- A window labeled "Signal Generator" should appear. Choose an AC sine wave
with amplitude 5.0 V and frequency 10 Hz. To change the frequency, click on
the number under "Frequency", type the desired number and the hit Enter.
- Click on. The speaker should respond. Click off.
- Mount the speaker to a stand a meter or so away from the edge of the
table, as shown below
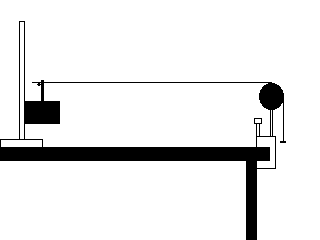
- Place the banana plug connector (red plastic thing with notch) so that it
is sticking out of the top of the speaker.
- On the edge of the table mount a universal clamp and to it a pulley. (You
can use a "smart" pulley, but there's no reason to plug it in.)
- Obtain the linear mass density (mass/length) of the thick stretchy cord.
(Take the knots out the get a good measurement of the length.)
Thick stretchy cord
String mass
( ) |
String length
( ) |
Linear mass density
( ) |
| |
|
|
- Then string it from the banana plug connector to the pulley and hang a
hanger and a weight on the end.
- Secure the cord with a knot just outside the plug or tie it to the stand.
- Turn the signal generator on. By varying the frequency, you should be able
to establish a standing wave pattern.
- Record the distance between nodes and the corresponding frequency.
- Find standing wave patterns with more nodes by increasing the frequency or
ones with fewer nodes by decreasing the frequency. Try to find at least four
different standing wave patterns.
Thick Stretchy Cord, Force ( ) =
Frequency
( ) |
Distance
between nodes
( ) |
| |
|
| |
|
| |
|
| |
|
- Vary the mass on the hanger and hence the tension F. Find a
standing wave pattern and measure the distance between nodes. (Whereas the
principle of keeping one variable fixed while you vary another is usually a
good idea, it doesn't work here. You will have to vary the frequency so you
can find a good standing wave pattern.)
- For each tension find two standing wave patterns. Repeat the measurements
for three more masses (five different tensions altogether). Record the
tensions and node-to-node distances. (Don't forget to include the mass of the
hanger.)
Thick stretchy cord
Force
( ) |
Frequency
( ) |
Distance
between nodes
( ) |
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
- Replace the stretchy cord with a piece of string and repeat all of the
above measurements.
Thin stretchy cord
String mass
( ) |
String length
( ) |
Linear mass density
( ) |
| |
|
|
Thin Stretchy Cord, Force ( ) =
Frequency
( ) |
Distance
between nodes
( ) |
| |
|
| |
|
| |
|
| |
|
Thin stretchy cord
Force
( ) |
Frequency
( ) |
Distance
between nodes
( ) |
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
Analysis
For both the thick and thin stretchy cord:
- For the first part in which the tension (force) was held fixed, make a
plot of the distance between nodes versus 1/frequency. Fit the
data to a straight line.
- What is another name for 1/frequency?
- How is the slope related to the speed of the wave in the string?
- How does the speed compare to the v = (F / m
)1/2 prediction?
Slope from graph
( ) |
Speed from graph
( ) |
Speed from (F / m )1/2
( ) |
Percent Error |
| |
|
|
|
- For the second part in which the tension was varied, use v = l / T to calculate the speeds. Then make a plot of the
speed versus tension. Fit it to a power law.
- How does the wave's speed depend on the tension in the string?
- How does this compare with the theoretical prediction?



 PYL 106: Standing Waves
on a string
PYL 106: Standing Waves
on a string 





