We focused on the Bohr model of the atom. We started with the Rutherford solar-sytem model with a positively charged nucleus and negatively charged electron orbiting. We recalled some of the things we have learned about planetary orbiting and tried to establish what would be the same and/or analogous in the solar system model of the atom.

Galileo put the sun at the center of the solar system/universe; the analogy here will be that the nucleus is at the center. Newton established with his Universal Law of Gravitation that orbital motion is just a special case of motion not unlike projectile motion, thus orbital motion boiled down to F=ma. We will take a simplified Oorbital motion to be circular. The motion involves changing direction, and hence centripetal acceleration, which is directed toward the center and has a magnitude of v² / r. For an atom, the force is not gravitational but electrostatic, and hence is given by Coulomb's Law: F = k q₁ q₂ / r². In the case of a Hydrogen atom one charge will be e (the charge of a proton) aand the other -e (the charge of an electron).

F_Coulomb = m a_centripetal

k e² / r² = m_e v² / r

which can be rewritten as

k e² = m_e v² * r

where we put the subscript e on the mass to indicate that it is the mass of an electron. (The direction (sign) has been accounted for; the force is toward the nucleus and so is the (centripetal) acceleration.

One problem with this early 20th model is that we know from Maxwell's equations that accelerating charges radiate. Thus this orbiting electron should emit electromagnetic radiation (energy) and spiral into the nucleus (more like a meteorite than a moon).

Kepler also had some results on orbits; the one of interest here is his second law -- the one about equal areas being swept in equal time. Recall we identified Kepler's Second Law previously as conservation of angular momentum.

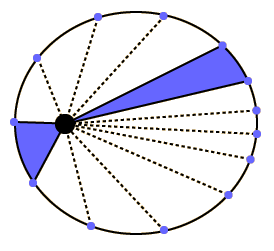
We suggested from this and our expression for linear momentum (mass * velocity) that the expression for linear momentum was: mass * velocity * radius. Note that if m * v * r is constant, then if v becomes larger, then r must become smaller.

Bohr suggested quantizing angular momentum: m * v * r = n ħ, where ħ = h / (2 π).  We can divide the equation m_e * v² * r = k e² by the equation m_e * v * r = n ħ in order to isolate v from r. This step yields:

v = k e² / (n ħ)

Substituting this expression back into either one of the previous equations and solving for r leads to

r = n² ħ² / (m_e k e²)

The above could be called the "atomic radius". The energy consists of two parts -- the kinetic energy m v²/2 and the electrostatic potential energy - k e² / r. Note the electrostatic potential energy has one r in the denominator as opposed to the Coulomb force with had r-squared. (They're related through an integral -- thnak you Isaac Newton and Gottfired Leibniz.)

E = m_e v² / 2 - k e² / r

Plugging in the expression for v and r into the above expression for energy results in

E = - m_e k² e⁴ / (N² ħ²)

The above result provide the "energy levels" for Hydrogem atoms. The lowest energy, n=1, is referred to as the groundstate. We posed the question: What other things are "Hydrogen like"? Two answers we came up with are 1) a Helium ion (what we have above does not deal with interactions between electrons, so Helium works if we throw away one if its electrons) and 2) Lithium (it has one "valence" electron)

Bohr produced the model of the atom we discussed previously, but in science we generally prefer to have some experimental verification.

Balmer

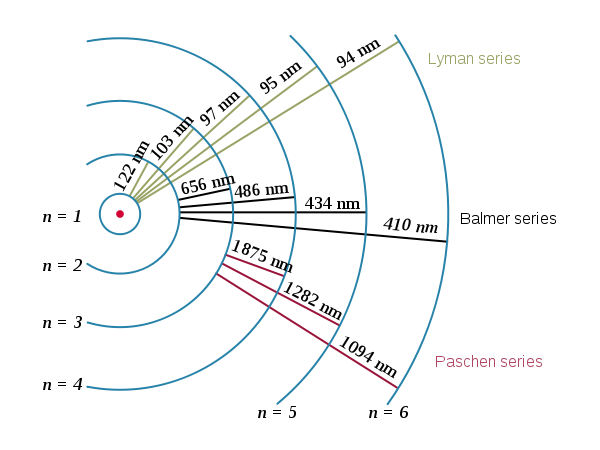
(from http://en.wikipedia.org/wiki/Hydrogen_spectral_series)

de Broglie, WAVE-PARTICLE DUALITY

Bragg

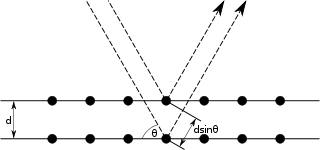
(from http://en.wikipedia.org/wiki/Bragg's_law)

Davisson-Germer

We will meet in the regular classroom and go over problems of the type that might appear on the test.